The DL_POLY Interface
The following chapter describes the molecular mechanics interface, which
allows the setting up of MM force-field expressions of the CHARMM, AMBER, GROMOS, UFF and
(approximate) MM2 types.
As for the other energy and gradient routines, this is accomplished by the
implementation of a family of routines, including
dl_poly.init, dl_poly.energy, and dl_poly.gradient (see description
of the general energy/gradient interface for more details).
Most of the arguments described below must be passed to the initialisation
function dl_poly.init and will be ignored if passed the energy and gradient
procedures.
Relationship to the DL_POLY Project
The implementation of the MM functionality makes use of some code
from the DL_POLY package
that is currently under development by
Dr W. Smith at CCLRC Daresbury Laboratory, and the
support of the authors of DL_POLY is gratefully acknowledged.
Users should note however that the interface described in this chapter
is not the one that will be used by the DL_POLY project and any bugs present
in the current implementation are most likely
to be result of errors in the interface and parameterisation, rather than DL_POLY itself,
and as such are not the responsibility of the DL_POLY project.
Not all of the features in the release of
DL_POLY_2 are available through the ChemShell interface, so this chapter
should not be regarded as a description of the functionality
of the DL_POLY package. For detailled infromation, there is an online version
of the manual
of DL_POLY_2 (pdf, 1.6 MB).
The table indicates the control arguments that may be passed to dl_poly.init.
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| coords= |
Fragment tag
|
yes |
none |
Initial configuration of the system |
| conn= |
Fragment tag
|
no |
use coords= |
Connectivity to use |
| mm_defs= |
file |
yes |
none |
specify file for force-field definition |
| use_pairlist= |
Boolean
|
no |
yes |
Use pairlist (alternative is all-pairs n**2 loop) |
| no_elec= |
Boolean
|
no |
no |
Electrostatic potential terms off |
| cutoff= |
real |
no |
99.99 Ang |
Cutoff for pairlist generation (in a.u.). In case
of periodic systmes, the default is half the cell size. |
| mxlist= |
integer |
no |
5000 |
Allocation parameter for pairlist, allow max(natoms,mxlist) entries per atom |
| mxexcl= |
integer |
no |
variable |
Allocation parameter for excluded atom list, may need to be increased for qm/mm calculations with a large qm region |
| exact_srf= |
Boolean
|
no |
no |
Evaluate short-range forces exactly, rather than using lookup tables. Not available for periodic systems |
| scale14= |
Tcl list of 2 integers |
no |
{1.0 1.0} |
Scale factors for electrostatic and VDW interactions, respectively |
| atom_types= |
Tcl List
|
no |
natoms*undef |
Atom type settings (undef means auto generate) |
| atom_charges= |
Tcl List
|
no |
natoms*unset |
Atom charges (unset means take forcefield value for the type) |
| debug_rank_e= |
Boolean
|
no |
off |
request ranked energy contributions debug |
| list_option= |
Output keyword
|
no |
full |
Output verbosity |
| debug_pairlist= |
Boolean
|
no |
off |
request tabulation of pair and excluded atoms list |
| debug_times= |
Boolean
|
no |
off |
print timing information |
| debug_memory= |
Boolean
|
no |
off |
request listing of size of DL_POLY arrays |
| ecut= |
real number |
no |
not applied |
maximum acceptable value for the energy |
| frozen= |
Tcl List
|
no |
none |
Specify a list of frozen atoms. Energy and force
contributions between such atoms are not calculated. This changes the total
energy by a constant amount. |
| groups= |
Tcl List
|
no |
none |
Specify a list of (ideally neutral) charge
groups. A list of lists, each sublist containing the atom numbers of atom
belonging to the group. Increases the accuracy of the electrostatic energy when
using a cutoff, see
electrostatics keywords. |
| spme= |
Boolean
|
no |
yes |
Use Smoothed Particle Mesh Ewald Summation to
calculate the electrostatics. If "no", standard ewald summation is used. This
keyword is ignored if no ewald sum is done, see
electrostatics keywords. |
| ewald_precision= |
integer |
no |
6 |
Set the estimated relative accuracy of the Ewald
(or SPME) summation to 10-N where N is spcified by ewald_precision. |
| suppress_ewald= |
Boolean
|
no |
no |
Set to yes for periodic systmes if you want to
suppress to calculate the electrostatics via Ewald summation. The default for
periodic systems is Ewald summation (SPME). |
| forcefield= |
keyword |
no |
none |
Use forcefield=uff to apply the UFF force field. |
The mm_defs argument specifies a file containing a keyword-based
definition of the force-field, and atom type information. For details
of the keywords that may be used see below.
The (optional) conn= argument is not required if the
connect function, invoked with the default tolerance settings,
produces a satisfactory connectivity for use in the parameterisation.
The (optional) constrain= argument at present may take only a single keyword
qc, and is used in the pre-optimisation of the MM part of
a QC calculation. It specifies that a set of harmonic
distance constraints be applied between pairs of atoms lying within
the qc part of the molecule. The use of this option required
that the qc part of the molecule be defined by applying the appropriate
attributes (qc and junction) to the atom types that represent QC atoms. The
harmonic force constant (atomic units) may be specified using the constrain=
argument.
Specifying the electrostatics
The treatment of the electrostatic interaction is generally the most demanding
part of a molecular dynamics simulation. Thus it requires special attention.
The following options are chosen depending on the provided keywords:
- Direct coulomb sum is used when no neighbour list is
calculated (use_pairlist=no). Accurate but demanding.
- Atomistic cutoff is used whenever a cutoff is specified and no
Ewald sum is done (see below). This option is NOT recommended, as it
leads to spurious energy changes when the neighbour list is updated (call to
dl_poly.update).
- Charge group implementation is used when neutral groups are
specified (groups=), a cutoff is used, and no Ewald sum is done. Pair
interactions are excluded on a neutral group basis. This method is recommended
whenever SPME is not possible.
- Ewald sum requires periodic systems. Used for
all periodic systems if spme=no and suppress_ewald=no (default).
- Smoothed Particle Mesh Ewald summation (SPME) requires periodic
systems. The most accurate and efficient method to calculate
electrostatic interactions. Recommended whenever possible, default for periodic
systems.
For further information, the reader is referred to the manual of DL_POLY
(pdf, 1.6MB).
CHARMM simulation mode
DL_POLY can take the topology and the force field parameters from a PSF file generated from
CHARMM and the corresponding parameter and topology files.
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| use_charmm_psf= |
Boolean
|
no |
no |
Whether to use topology (PSF) from CHARMM |
| charmm_psf_file= |
file |
yes (See note 1) |
- |
Topology (PSF) from CHARMM |
| charmm_parameter_file= |
file |
yes (See note 1) |
- |
CHARMM parameters (.inp format) |
| charmm_mass_file= |
file |
yes (See note 1) |
- |
CHARMM atomic masses (RTF format) |
Notes
1. These arguments are mandatory only if using a CHARMM PSF.
Using the CHARMM PSF will usually also require setting the
atom_types= and atom_charges= arguments.
It is sometimes helpful to read the connectivity from the CHARMM PSF file
into a fragment file (here charmm.c):
load_connect_from_psf charmm.c myfile.psf
If VMD is used to create the PSF file rather than the CHARMM program, the
PSF file results in XPLOR format. It can be read in by
read_xplor_psf atom_types= types atom_charges= charges atom_masses=
mass file= myfile.psf
which reads the
atom types into a variable called types, the
atom charges into a variable called charges, and the
masses into a variable called mass. These can subsequently used in
arguments to dl_poly as:
scale14 = { 1.0 1.0 } \
atom_types= $types \
atom_charges= $charges \
use_charmm_psf=yes \
charmm_psf_file= myfile.psf \
charmm_parameter_file= par_all27_prot_lipid.prm \
charmm_mass_file= top_all27_prot_lipid.rtf ]
AMBER simulation mode
DL_POLY can take the topology and the force field parameters from prmtop and
inpcrd files generated from AMBER.
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| amber_prmtop_file= |
file |
no |
no |
Whether to use topology (prmtop) from AMBER,
specifies the filename of the prmtop file |
To read the amber coordinates into a ChemShell fragment, the following
command can be used:
load_amber_coords inpcrd=<inpcrd file> prmtop=<prmtop file>
coords=<fragment name>
Setting up the Force Field
The following entries are made in the file specified by the
mm_defs option.
Defining the Atom Types
By default, elemental atom types are defined automatically, as is
a wild type (*) that may be used for general parameter assignment.
It is possible to define new atom types, and this is necessary for
the parameterisation of systems in which a number of inequivalent
environments exist for the same elemental type.
To facilitate the definition of the force field in terms of
generic and specific parameter types, a hierarchical definition
of atom types is used.
In general, definition of new types may be performed in response to
a number of keywords.
-
declare
- It is simply declared, with optional specification of a legal
connectivity count for items of this type.
It is simply declared, with optional specification of a legal
connectivity count for items of this type.
declare <type> <# conn> <# conn> ..
-
subgroup
-
It is simply declared as a subtype of an existing atom type, using the
subgroup keyword.
subgroup <existing-type> <type> <description>
e.g.
subgroup c ct ``Amber ca carbon type''
declares ct to be a new type, a subtype of c. The descriptive
string is used by the log file to identify the type.
-
supergroup
-
It is derived by combining a number of existing types using the
supergroup command.
Specifies that the new atom type is to be considered as a subtype
of an existing type.
supergroup <type>
- substructure query
-
It is defined using a substructure query. The substructure
query is specified by a group of keyword-type fields as follows.
Define a new atom type as a superset of existing groups.
group <type> <description> <type1> <type2> ..
Commence definition of an atom type.
query <type> <description>
Define an atom type specification that an atom must satisfy if it
is to be classified as a member of the type we are defining with this query.
This command effectively defines the first atom of the substructure query.
target <type>
This keyword adds another atom to the substructure query, to match the
atom must have the type specified.
atom <type>
Specify that a pair of atoms (denoted by their order of definition using target and
atom) must be connected for a substructure match.
connect <index1> <index2>
The atom types will be set up by default to the atomic types, or according to any
substructure-based rules you read in. It is usually simpler for a small molecule,
to define the atom types by hand, rather than to specify rules for automatic
typing.
Atom types are read in using the keyword types, followed by a list of types,
one for each atom.
The special type ``free'' may be specified, in which case the automatic types
will be used. Note that unless rules have been provided to distinguish
between atom types that refer to the same element, automatic typing will
fail.
A repeat count (of the form count*type ) may be used for brevity
when the same type applies to a number of consecutive atoms.
Specifying the Energy Terms
The following entries may be included in a file (specified by the mm_defs
argument) and serve to define a force field. In all cases, whether a given
term is used in the parameterisation of the molecule in question is a function
of the atom types assigned to the atoms of the molecule, and those present in the
force field definition.
The general rule is that if a group of atoms in the molecule have the
correct types and the correct pattern of connectivity to match the
force-field definition, then that force-field term will be applied
to those atoms.
- bond
-
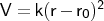
Format: bond
<type1><type2><k><r0>
The force constant <k> is specified in kcal mol-1 Å-2, and
the equilibrium distance <r0> in Å. It will be applied only to
connected pairs of atoms with atom types that are the same as (or subgroups of)
the types<type1> and <type2>.
- mm2bond
-
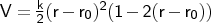
Format: bond <type1><type2><k><r0>
The force constant <k> is specified in mdyn Å-1, and
the equilibrium distance <r0> in Å. It will be applied only to
connected pairs of atoms with atom types that are the same as (or subgroups of)
the types<type1> and <type2>.
NOTE: Note that in this implementation no special precautions are taken to deal with the
steep fall in energy at long distances due to the cubic term. Poor structures should
be pre-optimised using a harmonic bond stretch forcefield first.
- quarbond
-
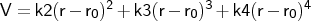
Format: bond
<type1><type2><k2><k3><k4><r0>
The force constants <kn> are specified in kcal mol-1 Å-n, and
the equilibrium distance <r0> in Å. It will be applied only to
connected pairs of atoms with atom types that are the same as (or subgroups of)
the types<type1> and <type2>.
- angle
-
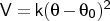
Format: angle <type1><type2><type3><k>
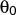
The force constant <k> is specified in kcal mol-1 rad-2,
and the equilibrium angle
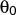 in degrees. It will be applied only to
connected sets of three atoms (connected 1-2-3) with atom types that are the same as (or subgroups of)
the types <type1>, <type2> and <type3>.
in degrees. It will be applied only to
connected sets of three atoms (connected 1-2-3) with atom types that are the same as (or subgroups of)
the types <type1>, <type2> and <type3>.
- ubangle
-
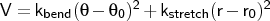
Format: ubangle <type1> <type2> <type3> <kbend>
<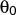 > <kstretch> <r0>
> <kstretch> <r0>
ubangle is used to define a combined harmonic bond angle term and Urey-Bradley term (1-3 harmonic non-bonded interaction).
The force constant <kbend> is specified in kcal mol-1 rad-2,
and the equilibrium angle
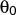 in degrees.
The force constant <kstretch> is specified in kcal mol-1 Å-2, and
the equilibrium distance <r0> in Å.
It will be applied only to
connected sets of three atoms (connected 1-2-3; note that <r> is the distance between the unconnected atoms 1 and 3)
with atom types that are the same as (or subgroups of)
the types <type1>, <type2> and <type3>.
in degrees.
The force constant <kstretch> is specified in kcal mol-1 Å-2, and
the equilibrium distance <r0> in Å.
It will be applied only to
connected sets of three atoms (connected 1-2-3; note that <r> is the distance between the unconnected atoms 1 and 3)
with atom types that are the same as (or subgroups of)
the types <type1>, <type2> and <type3>.
- mm2angle
-
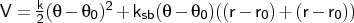
where r and r' denote the lengths of the bonds participating in the angle.
Format: mm2angle <type1><type2><type3><k>
The MM2 angle bend expression is used, and a stretch-bend interaction is added if
ksb is non-zero. It is an fatal error to input a mm2angle term for an angle a-b-c
if stretching terms for the a-b and b-c bonds are not also defined. The force constant
and stretch-bend constant are in the millidyne-based units used by MM2
(see JACS v99, (1977) p8130).
NOTE: The implementation is not exactly equivalent to that
implemented in the MM2 program, as the stretch-bend coupling term is
retained for angles involving H atoms (in MM2 such stretch-bend terms
are deleted).
- quarangle
-
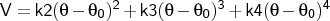
Format: bond <type1><type2><k2><k3><k4>
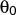
The force constants <kn> are specified in kcal mol-1 rad-n, and
the equilibrium angle
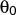 in degrees. It will be applied only to
connected sets of three atoms (connected 1-2-3) with atom types that are the same as (or subgroups of)
the types <type1>, <type2> and <type3>.
in degrees. It will be applied only to
connected sets of three atoms (connected 1-2-3) with atom types that are the same as (or subgroups of)
the types <type1>, <type2> and <type3>.
- ptor
-
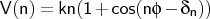
where
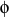 is the torsion angle.
is the torsion angle.
Format:
ptor <type1><type2><type3><type4><kn>
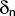 <n><key><flip flag>
<n><key><flip flag>
ptor is used to define a periodic torsional potential term, consisting
of a series of up to three cosine terms.
key determines the connectivity of the four atoms, and is used
when choosing sets of four atoms for which the potential will be
calculated, as shown in the table below.
| <key> |
connection |
Comments |
| i-j-k-l |
i-j, j-k, k-l |
conventional proper torsion angle |
| k-ijl |
k-i, k-j, k-l |
improper definition (as used in AMBER) |
| i-jkl |
i-j, i-k, i-l |
improper definition (as used in GROMOS) |
flip flag determines whether the torsional angle may be flipped,
or is defined in a fixed sense. The default value is 0, meaning it
may be flipped.
The angle is measured around the vector j-k.
If more that one record is provided with the same <type1>
-<type4> and<key> the parameters are combined to
give a composite torsional potential. No more than 3 terms may be specified for
a composite
potential.
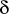 should be provided in degrees.
should be provided in degrees.
- mm2ptor
-
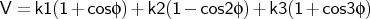
where
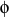 is the torsion angle.
is the torsion angle.
Format:
mm2ptor <type1><type2><type3><type4><k1><k2><k3>
mm2ptor is used to input a proper torsional potential of MM2 form.
The kn are given in kcal mol-1.
- mm2tor
-
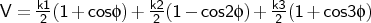
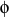 is the torsion angle.
is the torsion angle.
Format:
mm2tor <type1><type2><type3><type4><k1><k2><k3>
mm2tor is used to input a proper torsional potential of MM2 form.
The kn are given in kcal mol-1.
- htor
-
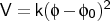
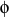 is the torsion angle.
is the torsion angle.
htor <type1><type2><type3><type4><k>
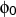 <key>
<key>
htor is used to define a harmonic torsion term, and usually used to
apply planarity or tetrahedral constraints.
The force constant <k> is specified in kcal
mol-1 rad-2 and 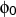 is in degrees. <key> specifies the
connectivity of the four atoms as indicated above for the ptor
definition.
is in degrees. <key> specifies the
connectivity of the four atoms as indicated above for the ptor
definition.
When the harmonic torsion parameters are applied to a given set of
four atoms, the value of
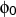 provided will be multiplied by -1.0 if doing
so reduces the computed energy of the initial configuration.
provided will be multiplied by -1.0 if doing
so reduces the computed energy of the initial configuration.
- cfftor
-
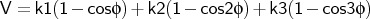
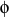 is the torsion angle.
is the torsion angle.
Format:
cfftor <type1><type2><type3><type4><k1><k2><k3><key>
cfftor is used to define the consistent force field torsional potential term.
key determines the connectivity of the four atoms, and is used
when choosing sets of four atoms for which the potential will be
calculated, as shown in the table above. The angle is measured around the
vector j-k.
- bb-ba-couple
-
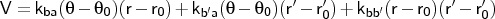
Format:
bb-ba-couple <type1><type2><type3><kba><kb'a><kbb'>
bb-ba-couple is used to input a generic bond-bond and bond-angle
coupling. The units of the force constants are kcal mol-1Å-1 rad-1 for the bond-angle terms and kcal mol-1Å-2 for the bond-bond coupling term. Note that the bond-angle
coupling terms may be discriminated between, contrary to the mm2angle term (see 1.4.3). Bond b is assumed to be between atoms of <type1> and <type2>; bond b' between atoms of <type2> and <type3>.
NOTE The program will create an error
if a regular angle or one of the bonds participating in the angle is
not specified prior to definition of the coupling term.
- aa-couple
-
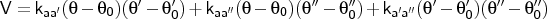
Format:
aa-couple <type1><type2><type3><type4><kaa'>
<kaa''>
<ka'a''>
aa-couple is used to input angle-angle coupling terms. The input
is organised as follows: the atom common to all angles is first (<type1>), followed by the connected atoms. Angle a is between<type2>-<type1>-<type3>, angle a' is between<type2>-<type1>-<type4>, and angle a'' is between<type3>-<type1>-<type4>.
NOTE The program will create an error if the regular angles
are not specified prior to definition of the coupling term.
- aat-couple
-
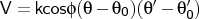
Format:
aat-couple <type1><type2><type3><type4><k>
aat-couple is used to input angle-angle-torsion coupling terms,
and the types are given as for proper torsion input (see
1.4.3). Angles
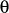 and
and
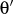 are between <type1>-<type2>-<type3> and <type2>-<type3>-<type4>, respectively.
are between <type1>-<type2>-<type3> and <type2>-<type3>-<type4>, respectively.
NOTE The program will create an error
if the regular proper torsion or either of the regular angles are
not specified prior to definition of the coupling term.
- vdw
-
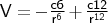
Format: vdw <type1><type2><c6><c12>
The units of <c6> are kcal mol-1 Å-6, those for <c12> are kcal mol-1 Å-12.
- powers
-
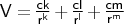
Format: powers <type1><type2><ck><cl><cm>
powers is used to input general 3-term power-law non-bonded potentials.
The units of <cn> are kcal mol-1 Å-n.
NOTE k,l, and m need not necessarily be integer numbers.
- m_n_vdw
-
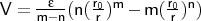
Format: m_n_vdw <type1><type2><m><n><r0>
<
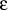 >
>
The units for <r0> are Å, and for
<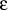 >
kcal mol-1.
>
kcal mol-1.
- exp_6_vdw
-
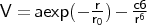
Format: exp_6_vdw <type1><type2><a><r0><c6>
exp_6_vdw is used for Buckingham (exp-6) type potentials.
<r0> is given in Å, <a> in kcal mol-1, and <c6> in kcal mol-1 Å-6.
- mm2_vdw
-
?????
Format: mm2_vdw <type1><type2><rvdw>
<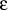 ><r0>
><r0>
mm2_vdw is a special keyword allowing the input of Buckingham (exp-6) type potentials
using the MM2 parameterisation.
<rvdw> is the sum of van der Waals radii for the two centres
in Å,
<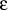 >
is an energy parameter (kcal/mol) and <r0> should be set to 0.0
until the shifted H-coordinates used in MM2 are implemented.
>
is an energy parameter (kcal/mol) and <r0> should be set to 0.0
until the shifted H-coordinates used in MM2 are implemented.
The Excluded Atom List
The excluded atom list in DL_POLY will include
- Those generated implicitly within DL_POLY from the presence of bond and angle
parameters. Note that it is the presence of an assigned parameter (rather than
a geometrical bonded contact). Therefore, if you decide you don't want to
include a MM bond term between two atoms, simply leaving the term out of
the definition of the force-field will result a short-range force and electrostatic
term being evaluated, which may not be what you want.
- Attributes of specific atom types (see below). These generate entries in
an internal table (printed in the listing), which is implemented by generating
zero force-constant bonds. These serve to avoid the inclusion of non-bonded
when parameters are systematically omitted, as in the case of hybrid calculations.
Specifying Attributes
The parameterisation may be modified by giving some of the
atoms or atom types specific attributes, which modify the parameters
assigned to atoms of the relevant type.
The attributes may be assigned either to the atom types, or to
the individual atoms.
To set the attributes associated with a given
atom type, use the keyword attribute.
attribute <atom-type> <attribute>
Setting attributes by atom : atom_attributes
To set the attribute for specific atoms, use the atom_attributes
keyword. This method of input is designed for cases where you wish to
associate either no attributes, or a single one, with each atom. One
attribute entry is given for each atom, the special attributes
``unset'' is used where no attribute is to be set. As for the types
keyword described above, you may use repeat counts of the form count*attribute.
atom_attributes <attribute list>
For example, to associate the qc attribute with the first 2
atoms of a 8 atom molecule, you could use:
atom_attributes 2*qc 6*unset
qc and junction
The attribute qc may be applied to designate an atom within the
QC part (QM part) of a hybrid QM/MM calculation (see the hybrid module).
The attribute junction may be applied to designate an atom which
lies within the QC part of a hybrid MM/QC calculation, but has
bonds to atoms described by molecular mechanics.
This will have the effect of partially suppressing the parameterisation
of atoms of the types that have the attributes specified.
No bond terms including two qc or junction atoms,
or angle terms with a qc or junction atom
in the central position will be included.
Proper torsion angles around bonds wholly within the QC component will
be deleted, as will improper torsional terms with a connectivity pattern
i-j-k-l.
Improper torsion terms with connectivity i-j,k,l or k-i,j,l
will be deleted if the cental atom (i or k respectively) is part
of the QC component.
An entry in the excluded atom list will be generated between all atoms
within the QC component, and between all pairs of atoms that are
bonded to the same junction atom.
exclude
The attribute exclude may be used to remove non-bonded forces
between a group of atoms by setting the exclude attribute for
all atom types in the group. All atoms with atom types
for which this attribute is set will have zero force-constant
bonds introduced to all other such atoms. This will force
MM to generate entries in the excluded atom list.
Specifying Charges
It is possible to change the charge used in the electrostatics
calculation either by setting a a charge associated with an atom
type, or setting the atomic charges individually.
This keyword sets the atomic charge associated with a given atom type.
charge <type> <charge>
The keyword atom_charges may be used to specify a list
of charges, to be applied to each individual atom. One
charge entry must be given per atom, the word ``unset'' should
be used for an atom if the charge is to be determined from
the atom type.
For example, the following record will set the MM charge of the
first atom to -1.0, the remainder will be have charges determined
by their atom type.
atom_charges -1.0 3*unset
Please note that the inclusion of electrostatic terms is
independent of the inclusion of the vdw (or similar)
short-range forces. They will be included for all charged
atoms unless an excluded-atom entry is preset (see above).
|
![]() should be provided in degrees.
should be provided in degrees.
![]()
![]() is the torsion angle.
is the torsion angle.
![]()
![]() is the torsion angle.
is the torsion angle.
![]()
![]() is the torsion angle.
is the torsion angle.
![]() <key>
<key>
![]() is in degrees. <key> specifies the
connectivity of the four atoms as indicated above for the ptor
definition.
is in degrees. <key> specifies the
connectivity of the four atoms as indicated above for the ptor
definition.
![]() provided will be multiplied by -1.0 if doing
so reduces the computed energy of the initial configuration.
provided will be multiplied by -1.0 if doing
so reduces the computed energy of the initial configuration.
![]()
![]() is the torsion angle.
is the torsion angle.
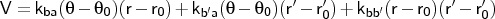
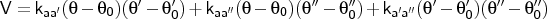
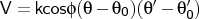
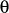 and
and
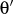 are between <type1>-<type2>-<type3> and <type2>-<type3>-<type4>, respectively.
are between <type1>-<type2>-<type3> and <type2>-<type3>-<type4>, respectively.
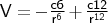
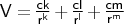
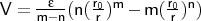
 >
>
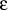 >
kcal mol-1.
>
kcal mol-1.
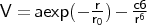
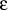 ><r0>
><r0>
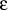 >
is an energy parameter (kcal/mol) and <r0> should be set to 0.0
until the shifted H-coordinates used in MM2 are implemented.
>
is an energy parameter (kcal/mol) and <r0> should be set to 0.0
until the shifted H-coordinates used in MM2 are implemented.