Programming Optimisation Schemes in Newopt

Introduction

The standard optimisation algorithms described above are written in terms of basic commands, which may be put to much more use in allowing the user to write his own Tcl script, which may contain things like if-statements and loops.

The most flexible way to use the package is thus to invoke the component commands directly from a Tcl script. To allow recursive or reentrant optimisation algorithms to be constructed, an object-oriented design has been adopted. An optimiser object is created using the optimiser command, the name of the object is then a valid Tcl command and methods are invoked by the syntax

$opt <method>

Where opt is set to the name of the optimiser object and <method< is the name of the required method. The optimiser's internal data is stored in two types of data structure

Control data is held in elements of the no_parm array.
Numerical data is help in ChemShell Matrix objects.

Different instances of the optimiser are distinguished by using the optimiser name in both cases: The variables are referenced using names of the form no_parm($opt,<param_name>) and the matrix names are prefixed by the optimiser name.

Method Args Function

px print current parameter position

sp test point as suitable restart point-tester is the RMS of the gradient

ss save the start structure (only for the zopt function, named zmatrix.start)

sr save the best available structure (only for the zopt function, named zmatrix.best)

wr name write object to file, attaching label. Valid labels are start, best, vis

f compute function value

g compute gradient

fdg compute gradient by finite-difference of energy

eg compute gradient without frozen hessian eigenmode contributions

fg compute function and gradient

gn get current gradient norm (into parm(gnorm))

grms get current gradient rms (into no_parm(grms))

tg test quality of gradient

ug transform gradient with hessian eigenvectors

h compute analytic hessian (for gamess only)

fdh generate hessian by finite differences of gradients with a one-point formula for all variables

fdh2 generate hessian by finite differences of gradients with a two-point formula for all variables

fd i generate hessian row and column for variable i by finite differences of gradients with a one-point formula

fd2 i generate hessian row and column for variable i by finite differences of gradients with a two-point formula

gh generate diagonal guess-hessian from simple rules

efdh i j ... modify hessian by finite-differencing along i'th, j'th, k'th, etc. hessian eigenmodes and back-transform the hessian

efdh2 i j ... modify hessian by two-point finite-differencing along i'th, j'th, k'th, etc. hessian eigenmodes and back-transform the hessian

sh m set hessian matrix from matrix m

shv i a set diagonal hessian value for variable i to a

mh condition hessian to have the correct inertia by massageing the eigenvalues

sih m set inverse hessian from matrix m

sh1 set hessian matrix to be the unit matrix

sih1 set inverse hessian to be the unit matrix

dh diagonalise hessian

sm set (first usage) or select (all subsequent usages) hessian eigenvector mode to be followed in TS search

sms set (first usage) or map (all subsequent usages) hessian eigenvector modes unto starting modes

um update hessian eigenvalue mode to be followed in TS search

hc determine the hessian inertia ( i.e. the number of positive, negative, and zero eigenvalues)

ih invert hessian

iih invert the inverse hessian

dih diagonalise inverse hessian

pu Powell-update the hessian

bfu BFGS-update the hessian

bfui BFGS-update the inverse hessian using the GAMESS-UK code

u0 BFGS estimate and first update of the inverse hessian

u BFGS-update the inverse hessian

msu Murtagh-Sargent-update the hessian

msui Murtagh-Sargent-update the inverse hessian

pmsu Hybrid Powell/Murtagh-Sargent-update the hessian

s take current step

ovls calculate overlap between current and previous step

rx reset the position vector to that of the previous step

sl s set step length to s

cl s calculate step length and set it to s if it exceeds s

clv s calculate search length and set it to s if it exceeds s

rs s restrict step, such that largest element equals s

tr determine trust region by comparing actual and predicted energy changes

ee estimate energy change from second-order model (valid hessian assumed)

gs set step vector to steepest descent direction

es iv set step vector to inverse hessian eigenvector iv

evs iv set step vector to hessian eigenvector iv

pfm i project i'th hessian eigenvector (mode) out of the step-vector

gda add current point to diis space

gdd i delete i'th (first point 0) point from diis space

gddg delete point with highest gradient rms from diis space

gdp print all current diis data points and gradients

gds evaluate diis step

gdw write diis space (points and gradients to files newopt.gdxr and newopt.gdgr, respectively

gdr m1 m2 read diis space from matrices m1 (points) and m2 (gradients)

cgr calculate conjugate gradient restart step vector

cg calculate conjugate gradient step vector (Shanno-Phua code)

cgs calculate conjugate gradient step vector

n set step vector by newton method

prfo calculate (p)rfo step vector

ls line search step

ls2 line search step with at least two trial points

lsf line search step with function values only

lsg line search step with function and gradient values

tc check for convergence

d diagnose the current point for sensibility

sym m symmetrize square matrix m

lv list current variables and their gradients

pun name append the current structure to punch-file name for viewing

praxis invoke PRAXIS optimizer

log print optimisation log (steps, line searches, updates)

x free memory

The above commands operate on a group of Matrix data structures, listed in the following table. In many cases it is not necessary to access the data explicitly--since an entire optimisation can be performed in terms of the operations given above. However, a series of Tcl commands are available if one wants to operate on the Matrix data structures directly.

Tag Dimensions Title

$opt.f 1 x 1 f (function value)

$opt.pf 1 x 1 pf (previous function value)

$opt.x n x 1 x (position vector)

$opt.px n x 1 px (previous position vector)

$opt.rx n x 1 rx (best restart position vector)

$opt.g n x 1 g (gradient vector)

$opt.pg n x 1 pg (previous gradient vector)

$opt.gd n x 1 gd (gradient difference [g - pg])

$opt.eg n x 1 eg (gradient vector for convergence test)

$opt.v n x 1 v (current search dir)

$opt.s n x 1 s (step vector)

$opt.ps n x 1 ps (previous step)

$opt.h n x n h (hessian matrix)

$opt.ph n x n ph (previous hessian matrix)

$opt.ih n x n ih (inverse hessian matrix)

$opt.evalh n x 1 evalh (eigenvalues of hessian matrix)

$opt.evech n x n evech (eigenvectors of hessian matrix)

$opt.ug n x 1 ug (transformed gradient vector)

$opt.m n x 1 m (mode-following vector)

$opt.mode n x 1 mode (mode vector)

$opt.modes n x n modes (modes (original hessian eigenvectors))

$opt.st n x 1 st (step vector from CG restart iter)

$opt.yt n x 1 yt (g(i) - g(i-1) from CG restart iter)

$opt.yi n x 1 yi (current g(i)-g(i-1))

NOTE: $opt.st, $opt.yt, and $opt.yi are defined only in a conjugate-gradient optimisation.

The following table describes the elements of the Tcl array no_parm that are used to control the operation of the primitive commands. The first series of elements may be set during the optimisation; the second series are generated by the various commands and may be accessed to control the optimisation. The default values, where given, are those applied in the control scripts, (as invoked by the newopt and hessian commands. When writing custom optimisation algorithms many will need to be set explicitly.

Element Usage Default

function function to be invoked

args Tcl list of arguments to be passed to the function

method type of calculation finite_difference ( hessian); bfgs ( newopt)

threshold threshold-value for recalculation of hessian for selected degrees of freedom

status Tcl return value 0

verbose output flag 0

del displacement in finite-difference formulae 0.001

maxstep maximum number of steps in search 200

conv_maxgrad maximum gradient convergence criterion 0.001

conv_rmsgrad RMS gradient convergence criterion 0.0002

conv_maxstep maximum parameter step convergence criterion 0.001

conv_rmsstep RMS parameter step convergence criterion 0.0002

toler_energy energy forced-convergence criterion 1.0e-10

list_variables full listing of variables after each step yes

step maximum step-length 0.3

lsopt type of line-search algorithm ls

ls_eps1 line-search convergence parameter 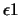$\epsilon1$ 0.9

ls_eps2 line-search convergence parameter 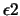$\epsilon2$ 0.001

trust_region vary maximum step length according to predictive power of the second-order model inactive

stepmin minimum step length with trust-region method 0.01

stepmax maximum step length with trust-region method 0.5

follow_mode hessian eigenvalue mode to be followed in TS search (use normal counting) 0 ( i.e. minimisation)

update_mode redefine mode to be followed to be the step taken off (keep starting mode)

hessian_update define update method of the hessian powell

fin_diff_eigenmodes recalculate part of the hessian by finite-differencing selected eigenmodes if inertia deteriorates no

keep_correct_hessian disregard update if hessian inertia deteriorates no

recompute_hessian number of steps after which hessian is to be recomputed maxstep+1 ( i.e. no recalculation of the hessian)

recompute_method method by which to compute the hessian finite_difference

condition_hessian hessian conditioning off

run_diagnostics check sensibility of the current point off

old_energy energy of previous point

new_energy energy of current point

best_step index of step with lowest RMS gradient

trust_steps number of steps taken without RMS gradient getting smaller 10

set_restart flag to write best restart structure after each step yes

thresh_prfo threshold for contribution of hessian eigenmodes to prfo step 1.e-4

conv_prfo convergence criterion for prfo shift parameter 1.e-4

contribute_prfo cutoff on hessian eigenvalue for contributing modes to prfo bracketing scheme 1.e-4

freeze_soft_modes flag for freezing near-zero eigenvalue hessian modes in Baker algorithm 0

soft_mode criterion on eigenvalue for considering a hessian eigenmode soft 1.e-3

freeze_modes flag for freezing selected hessian modes in Baker algorithm 0

mode_list Tcl list of indices of modes to freeze " "

min_diis_dimension minimum size of GDIIS space

max_diis_dimension maximum size of GDIIS space nvar/2

read_diis_space flag for reading in GDIIS matrices 0

diis_positions name of matrix with GDIIS positions " "

diis_gradients name of matrix with GDIIS gradients " "

maxlength maximum allowed step length 0.3

nvar number of degrees of freedom in the optimisation problem

hessian_ok indicator of correct hessian inertia no

best_hessian number of incorrect hessian eigenvalues

pos number of positive hessian eigenvalues nvar

gnorm gradient norm

grms gradient rms

map_modes Tcl list of map of current hessian eigenmodes on starting modes

Using The `method=custom` option

When a custom optimisation method is required, it can be passed in the form of Tcl list to the newopt procedure, as shown below. Note that the commands execute in a context in which the variable opt is set to the name of the optimiser object.

newopt function=$func method=custom \
	commands = { $opt fg; $opt gs; $opt ls; $opt u0; $opt n;
           while { [ $opt tc ] != 1 } { $opt ls; $opt u; $opt n; } 
        }

Constructing New optimisation procedures

It is sensible to use the optimisation algorithms within ChemShell for guidance, e.g. see chemsh/src/newopt/newopt_bfgs.tcl.

This manual was generated using htp, an HTML pre-processor

Programming Optimisation Schemes in Newopt

Introduction

Using The method=custom option

Constructing New optimisation procedures

Using The `method=custom` option