Finite Cluster Generation
Introduction
The ChemShell QM/MM procedures are most commonly used with finite
clusters, especially for highly polar materials where cutoffs cannot
be used.
Many of the systems to which QM/MM models are applied are condensed
phase in nature, and the simulation of such materials is often made
tractable by the use of periodic boundary conditions. However,
periodic boundary conditions are problematic for QM/MM simulations as
many QM codes (e.g. GAMESS-UK and MNDO) do not contain the ability to
compute the interaction of the QM system with an infinite charge
distribution. We have implemented a charge fitting approach which
enables a finite cluster to model accurately a single QM defect in an
infinite, perfect classical crystalline system. In many cases, this is
actually more pertinent to the real system under study than a model
system with a periodically repeating defect.
The approach adopted is
to start from the perfect, periodic system modelled using the
classical force field approach (Figure a), and from it cut a cluster
into which the QM model is to be embedded (b).
The electrostatic potential in the central active region is
computed (using the classical charge model) for both the perfect,
infinite system and for the finite cluster (ie (a) and (b) ). The
difference in these potential datasets represents the error introduced
by truncating the cluster.
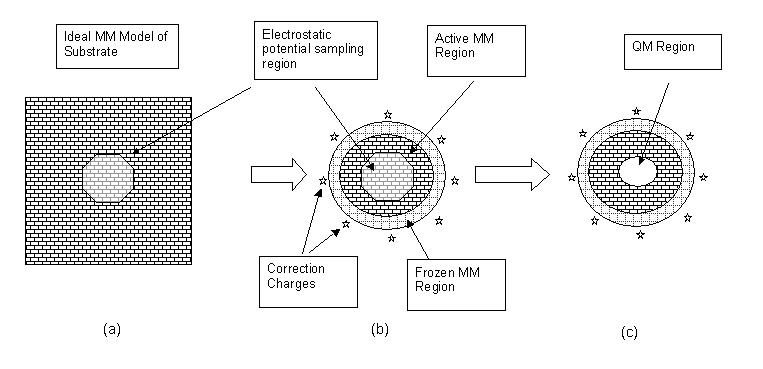
It is often possible to reduce the
magnitude of this error by adjusting the charges on the atoms on the
surface of the finite cluster. This is particularly true of covalent
solids where an adjustment can be applied for each bond cleaved by the
cluster generation.
The remaining error in the electrostatic potential can be corrected by
defining a set of additional point charges, placed around the outside
of the cluster.
The magnitudes of these charges are found by
least-squares fitting to the error potential so that they compensate
for the missing long-range electrostatic terms.
Finally the QM region can be defined (c), and with it a boundary
layer if required.
Setting up clusters with construct_cluster
The construct_cluster command is used to generate both spherical clusters from periodic
bulk systems and hemispherical surfaces from periodic slab systems. The nature of
the resulting cluster is determined automatically by the periodicity of the input crystal.
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| coords |
Fragment tag
|
yes |
- |
Fragment object defining the input crystalline system. Charges must be defined on all input atoms and shells. |
| cluster |
Fragment tag
|
yes |
- |
The resulting finite cluster. |
| crystal_type |
keyword |
yes |
- |
Type of bonding in crystal. Can be ionic, covalent (extended), or
molecular. |
| origin_atom |
integer |
yes (or origin_point) |
- |
Atom to define the centre of the cluster (centre of top face in surface case). |
| origin_point |
Tcl List
|
yes (or origin_atom) |
- |
Coordinates to define the centre of the cluster (centre of top face in surface case). |
| cluster_origin |
Matrix tag
|
no |
cluster_origin |
Name of object to store the cluster origin coordinates in for future reference. |
| radius_cluster |
real |
no |
40.0 |
Radius (in bohr) of the cut cluster. |
| radius_active |
real |
no |
20.0 |
Radius (in bohr) of the active MM region in the cluster. |
| bq_margin |
real |
no |
3.5 |
Distance (in bohr) between the cluster boundary and the outer point charges. |
| bq_density |
integer |
no |
5 |
Density of added outer point charges. The number of added point charges = (4 * bq_density^2) + 2 |
| bq_layer |
real |
no |
0.0 |
Height (in bohr) of extra point charge layers above the surface in the surface case. |
| bq_symbol |
string |
no |
F |
(Arbitrary) element symbol to assign to bqs for reference in MM codes. |
| adjust_charge |
keyword |
no |
none |
Specify a model for adjusting MM charges on the cluster boundary. Can be coordination_scaled or valence_model. |
| valence_matrix |
Matrix tag
|
no |
- |
Charge adjustment matrix for use with the valence_model scheme. |
| mm_theory |
string |
no |
- |
Option to define forcefield charges for periodic and cluster systems using an MM module. |
The construct_cluster process consists of three stages. Advanced users may wish to call these stages
independently, which can be achieved by using the Tcl commands in brackets:
- (cluster_cut) A bare cluster is cut from the periodic system. The size and origin is controlled by radius_cluster and origin_atom/origin_point. NB:
- If the valence model charge
adjustment scheme (see below) is selected, additional ions outside the cluster radius are included to
ensure that the cations are fully coordinated.
- In the case of crystal_type=molecular,
molecules are identified based on the fragment's connectivity and are either wholly included
or excluded from the cluster based on the average distance of the atoms in the molecule from the origin.
- Usually the input periodic system is specified including all charges, but alternatively an MM call
may be requested to assign charges using the mm_theory option
(as in the zeolite tutorial).
- (cluster_adjust_charge) Charges are adjusted at the boundary of the cluster. The simplest
scheme, coordination_scaled may be used with both bulk clusters and surfaces. In this case the
charges are scaled according to how many neighbours the boundary atoms are coordinated or bonded to.
In the valence_model scheme, the charges on the anions are determined based on their neighbours
according to the valence matrix (see below).
- (cluster_fit_bqs) Additional point charges are added around the outside of the cluster
to reproduce the missing electrostatic interaction from the bulk material. The number and position of the
point charges is controlled by bq_margin, bq_density and, in the surface case,
bq_layer. The fitting region is
defined by radius_active. The electrostatic potential of the bulk crystal is
evaluated using the Ewald method (periodic_electrostatics). The
resulting point charges are added to the cluster as atoms with the element symbol F. This is necessary
because MM codes such as GULP do not have a separate bq type. Your MM forcefield definitions
should use this symbol to define how the bqs behave. NB: If your cluster contains real
fluorine atoms, you should change the assigned bq symbol using bq_symbol.
In the valence model scheme, a valence matrix must be constructed which defines how the
anion charges are determined. Each row/column of the matrix corresponds to a species, which groups
atoms that share the same atomic number, charge, coordination and neighbour charges.
A list of species can be obtained using the periodic_species command:
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| crystal |
Fragment tag
|
yes |
- |
Fragment object defining crystalline system. |
| crystal_type |
keyword |
yes |
- |
Type of bonding in crystal. Can be ionic or covalent. |
The valence matrix can be created using the create_matrix command, e.g. for an MgO system
where species 1 is Mg(2+) and species 2 is O(2-), the appropriate valence matrix would be created by
create_matrix matrix=valence.dat datatype=real dimensions= {2 2} name=valmat {
0.0 0.333333333333333
-0.333333333333333 0.0
}
The matrix would then be passed to construct_cluster using the keyword valence_matrix=valence.dat.
Here the Mg ions will be assigned a +1/3 charge for each O neighbour, and the O ions
will be assigned a -1/3 charge for each Mg neighbour. However, note that in the valence model
scheme the cations are fully coordinated, so all Mg ions will have a full +2 charge.
If the shell model is used, the charges on the cores and shells will be scaled appropriately, i.e.
by the assigned charge divided by the total species charge.
Partitioning ionic clusters into regions with cluster_partition
ChemShell studies of ionic clusters generally use GULP as the MM code and use a cluster
model which is partitioned into five regions (QM, QM/MM interface, active MM,
inactive MM and point charges). Once the cluster has been generated, the cluster_partition
command can be used to define the different regions by assignment of labels with
a different integer suffix. Before calling the command the QM region should be defined
by adding the suffix '1' to the QM atom labels.
The labelling of the regions on the output is as follows:
- 1 - QM region
- 2 - QM/MM interface
- 3 - Active MM region
- 4 - Inactive MM region
- 5 - BQ (point charges)
The command line arguments to cluster_partition are:
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| coords |
Fragment tag
|
yes |
none |
Input coordinates. Atoms to be in the QM region
should have a label ending with 1 (eg Mg1, O1). |
| output |
Fragment tag
|
yes |
none |
Output coordinates of partitioned cluster. |
| cluster_origin |
Matrix tag
|
yes |
none |
Matrix containing coordinates of the cluster origin (output from construct_cluster). |
| cutoff_boundary |
real |
no |
10.0 |
Atoms within this distance (in bohr) from region 1 are assigned to region 2. |
| radius_active |
real |
no |
20.0 |
All atoms within this radius (in bohr) from the origin are assigned to
region 3 (active MM). |
| qmmm_interface |
string |
no |
implicit |
Choice of implicit or explicit QM/MM interface (see notes below). |
| interface_exclude |
Tcl List
|
no |
- |
List of atom symbols to exclude from the interface region. |
| interface_rigid |
Tcl List
|
no |
- |
List of atom symbols to be rendered rigid
in the interface region. For use with the explicit interface only. |
| bq_symbol |
string |
no |
F |
Symbol assigned to bqs by construct_cluster. |
The resulting region specifications are encoded into
the fragment file specified by output= by modification of the atom labels;
the region number is appended to the element symbol.
This can be used to control
forcefield and basis specifications for the QM/MM calculation.
There are two definitions for the QM/MM interface region (region 2)
that can be selected: implicit (the default) and explicit.
In the implicit interface, interface atoms are represented
in the QM calculation as QM atoms with ECPs attached.
In the explicit interface, the interface atoms are represented as bqs with ECPs
attached in the QM calculation and full core-shell MM atoms in the MM calculation
(if the shell model is being used).
Important: the choice of interface determines the number of electrons that should be replaced
by the ECP in the QM/MM calculation.
When using the implicit interface the ECP charge should be equal to the formal
charge of the ion (e.g. 10 for Mg2+). With the explicit interface, the ECP
charge should be set to 0 in general.
In addition to the relabelling, the cluster_parition command also removes the shells from
atoms in the quantum region, as these are not used
in subsequent QM/MM calculations. When using the implicit interface, shells are also
removed from region 2. Shells are generally kept in the interface region
when using the explicit interface, although ions in the interface region can be
selectively converted into rigid ions using the interface_rigid option. In this case
the charge on the shell is transferred to the core.
By default all species may enter the QM/MM interface region. Elements can be selectively
excluded from region 2 using the interface_exclude option. This can be useful to exclude
for example anions, either because an appropriate ECP is not available or because the
QM code does not support anion pseudopotentials.
For advanced ECP handling options, see the separate_boundary_ecps option in the hybrid module.
Region queries with get_cluster_region
When performing a QM/MM calculation the QM region must be explicitly specified. In
a QM/MM optimisation the active region must be specified as well. This information
can be queried from a partitioned cluster using the get_cluster_region command.
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| coords |
Fragment tag
|
yes |
- |
Fragment containing the partitioned cluster. |
| region |
keyword |
yes |
- |
Region query. |
The region query can be a list of region numbers or:
- qm_explicit - region 1 only (explicit interface)
- qm_implicit - regions 1 and 2 (implicit interface)
- active - regions 1-3
- atoms - regions 1-4
- all - regions 1-5
|
![]()