STFC
MPI für Kohlenforschung

University College London

QM/MM Free Energy Perturbation Calculations

Free energy perturbation (FEP) calculations at the QM/MM level can be set up manually or via the QM/MM-FEP module.

Manual set up of QM/MM FEP calculations

The following steps have to be done in order to use FEP on the QM/MM level in analogy to J. Chem. Phys. 112, 3483 (2000) and J. Chem. Theory Comput. 2, 452 (2006).
  1. Choose a reaction coordinate, one of those that can be constrained in the optimisation.
  2. Optimise a series of structures along this reaction coordinate.
  3. Calculate ESP charges for the QM atoms for each of these structures (see example below on how to do that with ChemShell).
  4. Run FEP calculations with each step perturbed with the step following in the reaction and backwards perturbed with the step preceeding in the reaction. The QM-part of the system will be fixed during the FEP sampling, the MM part moves. It is sufficient to calculate the electrostatic QM/MM interactions with the density replaced by ESP charges. Thus use qm_theory=pointcharge. All other parameters of the calculation should be the same as in the optimisation. 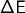$\Delta E$ of the perturbation will be written in the file qm_mm_orig_perturbed.dat.
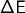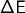  5. Run an MD to obtain a canonical average of $\Delta E$ . During this MD, the QM part is kept frozen. To ensure that also the link atoms are frozen, freeze the first MM atom of each link (junction atom). In each perturbation, the geometry of the QM part is replaced with the one of the perturbing QM-part. The difference in QM/MM interaction energy is $\Delta E$ .
  6. Analyse the obtained 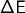$\Delta E$ using fep_convert.f90. It can be found in the directory contrib/. For this analysis, the electrostatic interaction energy between the QM-part and the MM-part in the optimised structures has to be known. It can be obtained by single-point calculations with qm_theory=pointcharge.

Explanation of the keywords and files:

npert: Number of perturbations: 0 for no FEP, 1 for forward perturbation only, 2 for forward and backward perturbation.

fep_linkmethod: Determines how a link QM-L-MM is perturbed. 1: only the QM atom is perturbed. 2: the QM atom is perturbed, the link atom is placed in line between the QM atom and the unperturbed MM atom. 3: QM and L are perturbed. 4: all three atoms, QM, L, and MM are perturbed. 1 and 2 use a position of the link atom which is inconsistent with the position, the ESP charge has been calculated for. In case of the full density (using a real QM method) this leads to violation of the ortho-normality of the wave function. Method 3 is inconsistent with the general link atom placement. Thus fep_linkmethod=4 is recommended.

fep_qm_theory: One can use the full density in FEP sampling, although an approximation by ESP charges will often be justified. A full QM calculation for each MD step, however, may be quite demanding. Therfore it is convenient to skip the SCF iterations and keep the density fixed. This is possible for qm_theory=mndo. In principle, also full SCF calculations may be performed. For that purpose it is possible to use a different method for the dynamics (gradient) than for the FEP. Thus the energy difference of the perturbation may be calculated more accurate than the trajectory. Using fep_qm_theory defines the QM theory used for the FEP calculations. The specified qm_theory is used for the gradient defining the trajectory.

Structure files: FEP needs the structures and the ESP charges or density matrix files of the perturbing structures. Thus a file called hybrid.$fep_qm_theory.coords_forward (e.g. hybrid.mndo.coords_forward) is required for link methods 1 and 3. A file hybrid.$mm_theory.coords_forward is required for link methods 2 and 4. It is the ChemShell fragment of the forward perturbing structure. ESP charges or densities are also provided by the corresponding files. Names: charges.c_forward for pointchage (can be changed with fep_denmat), fort.11_forward for MNDO, mos_forward for turbomole. They should be copied from the result of the optimisation. For backward perturbation, the corresponding files with _backward appended have to be provided.

The main output file of FEP is qm_mm_orig_perturbed.dat. In case of forward perturbation only it contains 4 columns, otherwise 6. The first two columns are QM and MM energy of the unperturbed system, respectively. Columns 3 and 4 are QM and MM energy of the forward perturbed system. Columns 5 and 6 are QM and MM energy of the backward perturbed system.

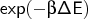This file may directly be used to analyse the results. It may be more convenient to analyse them using the fep_convert tool which can be found in the contributions of ChemShell. fep_convert -h provides explanations. It performs statistical tests on the equilibration of the calculation and then averages $exp(-\beta\Delta E)$ using the cumulant (k-statistics) expansion. 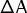With A being the free energy, $\Delta A$ may be obtained by 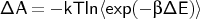$\Delta A = -kT ln \langle exp(-\beta\Delta E)\rangle$ . This 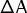$\Delta A$ refers to the free energy of the QM/MM interaction and MM terms only. The QM-energy difference, with the electrostatic QM-MM interaction removed, has to be added.

Example of FEP calculations

Calculate esp charges with: 
# declare the object to make it faster ...
fragment hybrid.mndo.coords old persistent

set mndo_args [ list hamiltonian= am1  \
					 charge= 1 maxcyc= 500 \
					 accuracy= high binary= 1 \
 	        grid=gridmat.c \
		coords=hybrid.mndo.coords \
]
# declare to make it persistent
fragment charges.c new persistent

mndo.init $mndo_args
get_esp_points coords=hybrid.mndo.coords grid=gridmat.c type=mmatoms
mndo.potential $mndo_args 
set_molecule_charge coords=hybrid.mndo.coords charge= 1
fit_esp_charges coords=hybrid.mndo.coords grid=gridmat.c store=charges.c
mndo.kill

# charges.c is once declared in fit_esp_charges and once here,
# so we have to delete it twice!
delete_object charges.c
delete_object charges.c

# This energy will be needed when processing the FEP data
energy coords=hybrid.mndo.coords theory=pointcharge

delete_object hybrid.mndo.coords

The actual FEP calculations will be done (after extensive equilibration, ...) by something like: 
set model [ list \
   npert=2 fep_denmat= charges.c \
   qm_theory=  pointcharge: charges_frag=charges.c \
   qm_region= $qmatoms \
    [ other hybrid arguments ]
 ]

# declare to make it persistent
fragment charges.c old persistent

dynamics dyn1 \
  theory=hybrid : $model \
  frozen= { 1-10 }
  ...
Make sure that all QM atoms and the MM atoms of the links are frozen. Otherwise pointcharge would produce an error message (and the results would be wrong!)

The QM/MM-FEP module

The approach to perform QM/MM-FEP calculations that was presented in the preceding section is very versatile. However, the price for this versatility is a considerable amount of manual work that is connected with QM/MM-FEP calculations. Therefore, the qmmmfep module was developed that automatises most of the manual work. The qmmmfep module performs all steps of a QM/MM-FEP calculation and computes the free energy difference between two structures. These two structures should be neighboring windows that result from a potential energy profile scan by means of a defined reaction coordinate.

The qmmmfep module:

  • computes the ESP charges of the QM atoms of the initial structure and the perturbing structure(s),
  • runs an MD simulation to sample the energy differences and checks the results for convergence,
  • computes the QM energy differences of the polarised wave functions without electrostatic QM-MM interactions, and
  • summarizes the results and outputs the free energy difference.

To perform these tasks, the qmmmfep module needs information about

  • the details of the FEP approach,e.g. the link method, the number of points used in fitting the ESP charges, etc.
  • the QM/MM approach that is used. The QM method will be used to compute ESP charges and QM energy differences. The MM method is used to sample over the MM degrees of freedom with pointcharge as QM method.
  • the information that the dynamics module needs to perform the MD simulation

These information has to be passed to the qmmmfep module via the following keywords:

Explanation of QM/MM-FEP keywords

coords: If the free energy difference between two structures i and i+1 is to be calculated, the name of the fragment object containing the coordinates of structure i has to be provided by the coords keyword.

coords_forward: The name of the fragment object containing the coordinates of structure i+1 has to be provided by the coords_forward keyword. In contrast to the QM/MM-FEP calculations via the dynamics module (see above), the qmmmmfep module always uses a fragment object of the full system to define the perturbing structure independent of the link method.

coords_backward: If the free energy difference to the preceding window i-1 is to be calculated in addition, the coordinates of this structure has to be provided via the coords_backward keyword. If input is given to this keyword, sampling of the backward perturbation is performed automatically.

esp_npoint: This keyword defines the number of external points around the QM region where the electrostatic potential is computed for fitting the ESP charges. Since the ESP are employed to represent the QM charge density in the MD simulation, the qmmmfep module always uses the nearest MM atoms. The shell model cannot be used.

fep_linkmethod: The postioning of the link atoms in the perturbed structure is ambiguous. Four different options are implemented in the ChemShell and were explained in the previous chapter (see above). fep_linkmethod= 4 is recommended.

equilibration_steps: In many cases it is advantageous to equilibrate the system before sampling energy differences. The number of equilibrating MD steps can be defined via the equilibration_steps keyword. The real equilibration time is defined in combination with the timestep keyword that has to be provided to the dynamics module via the dynamics_args keyword.

fep_minstep, fep_maxstep, fep_convcheck: Statistical tests are employed in the FEP sampling to check for a lack of trend and correlation. These tests are documented in J. Chem. Theory Comput. 2006, 2, 452-461 and J. Chem. Phys. 1985, 83, 5203. The qmmmfep module performs these tests automatically at defined intervals and stops the FEP sampling when convergence is achieved. However, these tests may yield false positive results if very little data is sampled. Therefore, a sufficient amount of data should be acquired before checking the first time. The number of data points that is sampled before the first test can be defined by the fep_minstep keyword. To avoid that the FEP sampling runs extremely long in problematic cases, a maximum number of FEP steps can be defined by the fep_maxstep keyword. The interval for checking for convergence is defined by the fep_convcheck keyword. The ouptut of the analysis procedure is written to fep_conv.out.

theory: The level of QM/MM theory has to be defined by the theory keyword. The qmmmfep module accepts only hybrid as input to this keyword. However, the subsequent input to the hybrid module defines the exact QM/MM method that is used in the QM/MM-FEP calculations. The defined QM/MM Hamiltonian is employed to compute the ESP charges of the QM regions and the polarised QM energy differences. Moreover, the MM theory defined by theory is used in the FEP sampling in combination with pointcharge as QM method.

dynamics_args: Although the dynamics module is called automatically by the qmmmfep module to perform the FEP sampling in an MD simulation, much of the input to the dynamics module has to be specified by the dynamics_args keyword. The only keywords that are set automatically by the qmmmfep module are coords, npert, fep_linkmethod, and fep_qm_theory. The rest of the input that is necessary for a sensible MD simulation has to be provided via the dynamics_args keyword.

Summary: The qmmmfep module does a single-point calculation at the QM/MM level of theory defined by theory and computes the ESP charges of the initial and the perturbed structures. It then starts an MD simulation with a number of equilibrating steps (equilibration_steps) followed by an FEP sampling of at least fep_minstep data points which is checked every fep_convcheck steps for convergence and stops automatically after fep_maxstep FEP steps or earlier if convergence is reached. Finally the qmmmfep module computes the QM energy differences of the polarised wave functions and assembles the total free energy differences.

Summary of QM/MM-FEP keywords

Argument Argument type Mandatory Default To specify
coords= Fragment tag yes n/a Fragment object containing the coordinates
coords_forward= Fragment tag yes n/a Fragment object containing coordinates of the forward perturbing structure
coords_backward= Fragment tag no n/a Fragment object containing the coordinates of the backward perturbing structure. Backward perturbation is computed automatically if coords_backward is defined.
esp_noint= integer no 200 Number of closes MM atoms that are used as reference points when fitting the ESP charges
fep_linkmethod= integer no 4 Method of link atom perturbation (see above)
equilibration_steps= integer no 1000 Number of initial MD steps to equilibrate the system before sampling energy differences.
fep_minstep= integer no 2000 Minimum number of FEP steps performed before results are checked for convergence
fep_maxstep= integer no 20000 Maximum number of FEP steps performed. The MD is stoped if convergence is not reached when this number is reached.
fep_convcheck= integer no 500 Interval of FEP steps to check for convergence
theory= Tcl List yes n/a QM/MM Hamiltonian used to compute the QM energy difference and the ESP charges. The MM method is used with pointcharge as QM method in the MD part of the calculation.
dynamics_args= Tcl List yes n/a All arguments that should be passed to the dynamics module and which are not set automatically by the qmmmfep module.

Example of QM/MM-FEP input

qmmmfep \
        coords= ${sys_name_id}.c \
        fep_linkmethod= 4 \
        esp_npoint= 200 \
        coords_forward= ${sys_name_id}.for.c \
        fep_skip= 1 \
        fep_convcheck= 100 \
        fep_maxstep= 15000 \
        fep_minstep= 10000 \
        equilibration_steps= 10000 \
        theory= hybrid : [ list \
                        coupling= $embedding_scheme \
                        cutoff= 200 \
                        groups = $groups \
                        atom_charges= $charges \
                        qm_region= $qmatoms \
                        qm_theory= $qm_theory : [ list \
				... 
				] \
                        mm_theory= dl_poly : [ list \
				...
				] \
       dynamics_args = [ list \
                temperature= 300 \
                nosehoover=4 \
                taut= 0.02 \
                timestep= 0.001 \
                trajectory_type= 1 \
                constraints= $con \
                masses= $masslist \
                frozen= $frozen_atom_numbers ]

As with the manual FEP method, the QM region and any connecting MM (linked) atoms must be frozen during the dynamics, here by specifying them in $frozen_atom_numbers.

This manual was generated using htp, an HTML pre-processor Powered by htp