DL-FIND
1. Introduction
DL-FIND is a powerful and flexible geometry optimisation library and
is the recommended optimiser module in ChemShell.
The code is under active development but the features
documented here are those that are available in the version distributed with ChemShell.
DL-FIND can also be downloaded as a standalone library from the CCPForge repository.
DL-FIND supports a wide variety of optimisation methods.
Standard local minimisation techniques are supported
(steepest descent, conjugate gradient, Newton-Raphson, BFGS) as well as damped dynamics and
limited memory BFGS (L-BFGS). Transition state methods include nudged elastic band (NEB)
for finding reaction paths and P-RFO and the dimer method for refining transition states.
Conical intersection optimisations are supported using penalty function, gradient projection
and Lagrange-Newton algorithms. Parallel optimisation methods include a genetic algorithm,
stochastic search and parallel NEB.
DL-FIND accepts input structures in Cartesian coordinates. These may be converted
into a number of internal coordinate systems for the optimisation, including
delocalised internal coordinates (DLCs), total connection, and hybrid delocalised
internal coordinates (HDLCs) for large systems. Constrained coordinates are supported
as well as a general mechanism for imposing restraints.
A detailed description of DL-FIND's features can be found in:
Johannes Kästner, Joanne M. Carr, Thomas W. Keal, Walter Thiel, Adrian Wander and Paul Sherwood, J. Phys. Chem. A, 2009, 113 (43), 11856-11865. DOI: 10.1021/jp9028968
Please cite this paper if you use DL-FIND in published work.
2. Command line arguments
2.1 General options
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| theory |
string |
no |
mndo |
Module used to compute energy and forces |
| coords |
Fragment tag
|
yes |
none |
Initial configuration of the system |
| result |
Fragment tag
|
no |
dl-find.result |
Optimised coordinates |
| coords2 |
Fragment tag
|
yes (for NEB) |
none |
Initial second configuration of the system. End
point of the initial path in NEB calculations, direction of the dimer in dimer
calculations. Can also be a list of fragments. Then it defines points along the
initial NEB path (the desired endpoint should be given last). |
| result2 |
Fragment tag
|
no |
none |
Optimised second coordinate set. Its contents
depend on the task. Usually a transition mode. |
| tsrelative |
Boolean
|
no |
false |
coords2 and result2 are specified relative to
coords and result, respectively |
| maxcycle |
integer |
no |
100 |
Maximum number of optimisation cycles |
| maxene |
integer |
no |
10000 |
Maximum number of energy and gradient evaluations |
| dump |
integer |
no |
0 |
Write restart information every dump
steps (0: never). |
| restart |
Boolean
|
no |
false |
Restart from a dump file. |
| list_option |
Output keyword
|
no |
medium |
How much output to generate (including generation of .xyz files) |
Setting list_option=full for a standard minimisation will output a
path.xyz file containing the optimisation trajectory and
path_active.xyz containing only the active atoms. Other methods
will generate other .xyz files as appropriate (see below).
2.2 Coordinate system options
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| coordinates |
keyword |
no |
cartesian |
Which coordinate system to use. Can be
cartesian, mass, dlc, tc,
hdlc, or hdlc-tc. |
| residues |
Tcl List
|
no |
none |
Definition of residues (fragments) for the option
coordinates=hdlc. See HDLCs. |
| frozen |
Tcl List
|
no |
none |
Specification of the atoms to be
frozen. Complementary to active_atoms |
| active_atoms |
Tcl List
|
no |
all atoms |
Specification of the atoms to be optimised. |
| constraints |
Tcl List
|
no |
none |
Constraints specification for use with internal coordinates. |
| restraints |
Tcl List
|
no |
none |
Restraints to apply |
| connect |
Tcl List
|
no |
none |
Add user-defined connections, format: { atom1
atom2 } |
The keyword coordinates specifies the coordinate system in which the
optimisation should be performed. Possible choices are:
- cartesian: Cartesian coordinates
- mass: Mass-weighted Cartesian coordinates
- dlc: Delocalised internal coordinates. A redundant set of bonds,
angles, torsions, and sometimes inversions is created. A non-redundant combination
of them is found by diagonalising the spectroscopic G-matrix. The
optimisation is performed in this non-redundant set.
- tc: Same as dlc, but the redundant set consists only of bonds—all
atoms in the system are connected (total connection scheme).
- hdlc: Hybrid delocalised internal coordinates. The system is
partitioned into fragments. Delocalised coordinates (as in DLC) are used
within each fragment. The fragments are coupled via Cartesian
coordinates. This version is recommended for large systems, as the
coordinate transformation scales linearly with the number of atoms.
- hdlc-tc: Hybrid delocalised internal coordinates based on the
total connection scheme.
Note that the dlc option is not equivalent to specifying hdlc with a single residue. The dlc case gives pure internal delocalised coordinates (6 external degrees of freedom are dropped), whereas with hdlc Cartesian coordinates are added to the primitive list even if there is only one residue, and the external degrees of freedom are retained.
2.3 Optimisation algorithm options
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| optimiser |
keyword |
no |
lbfgs |
Specifies the optimisation algorithm. Can be
lbfgs, prfo, cg, sd,
dyn, nr or ln. |
| trustradius |
keyword |
no |
constant |
Specifies the trust radius approach. Can be
constant, energy, or gradient. |
| maxstep |
real |
no |
0.5 |
Maximum change of one coordinate component in one
optimisation step. |
| tolerance |
real |
no |
0.00045 |
Convergence criterion for the maximum gradient
component. The criterion for the maximum step component is 4*tolerance,
for the RMS step it is 8/3*tolerance, for the RMS gradient it is
2/3*tolerance. All criteria are applied in the coordinate system
specified by coordinates. |
| tolerance_e |
real |
no |
tolerance/450 |
Convergence criterion for the energy change (in Hartree). |
| lbfgs_mem |
integer |
no |
DOF |
The number of steps kept in the L-BFGS
memory. Default: number of degrees of freedom. |
| initial_hessian |
keyword |
no |
external |
Type of Hessian to calculate at the start or when resetting. Can be external, onepoint, twopoint, diagonal, or identity. |
| update_method |
keyword |
no |
bofill |
Update algorithm for the Hessian
(e.g. in P-RFO TS search or quasi-Newton optimisation). Can be
bofill, powell, bfgs, or none. |
| delta |
real |
no |
0.01 |
Step size in the finite-difference Hessian calculation. |
| maxupdate |
integer |
no |
50 |
Maximum number of Hessian updates before the
Hessian is recalculated. |
| soft |
real |
no |
0.005 |
Eigenmodes with an absolute Eigenvalue below
soft are ignored by the P-RFO optimiser. This avoids movements in the
translation and rotation direction. A maximum of 6 modes are ignored. No modes
are considered soft when internal coordinates are used. |
| minstep |
real |
no |
0.00001 |
If the step size is below minstep,
the Hessian is not updated (to avoid problems with noisy gradients). |
| scalestep |
real |
no |
1.0 |
Scale the step obtained from SD or CG algorithms. |
| distort |
real |
no |
0.0 |
Distort the starting geometry along coords2 (if
positive) or against it (if negative). This may be useful when starting from a
TS and searching for minima. |
| timestep |
real |
no |
1.0 |
Time step (in a.u.) for damped molecular dynamics
(optimiser=dyn). |
| fric0 |
real |
no |
0.3 |
Start friction for damped molecular dynamics
(optimiser=dyn). |
| fricfac |
real |
no |
0.95 |
Factor to reduce the friction if the energy
decreases in damped molecular dynamics
(optimiser=dyn). |
| fricp |
real |
no |
0.3 |
Friction to apply if the energy increases in
damped molecular dynamics
(optimiser=dyn). |
The keyword optimiser specifies the optimisation algorithm. Possible
choices are:
- lbfgs: Limited-memory
Broyden–Fletcher–Goldfarb–Shanno optimisation. Recommended
for minimum search, NEB, and the dimer
method. The time and memory requirements spent for determining the search
direction and step length scale linearly with the system size. The number
of steps kept in memory is specified by lbfgs_mem.
- prfo: The partitioned rational function optimisation
method. Recommended for transition state search
(unless done by the dimer or NEB methods). It requires the calculation of
the Hessian. The keyword update_method can be used to specify how the
Hessian should be updated.
- cg: Conjugate gradient method following Polak–Ribiere.
- sd: Steepest descent.
- dyn : Damped molecular dynamics. Four
additional parameters can be
specified. timestep is the time step in atomic units. fric0
is the start friction, fricfac is the factor to reduce the friction
each time the energy decreases, and fricp is the friction to apply if
the energy increases. The frictions are defined so that 0
corresponds to free (undamped) dynamics, and 1 corresponds to steepest
descent. This variable friction facilitates convergence to an energy minimum.
- nr: Basic Newton-Raphson/quasi-Newton optimiser.
- ln: Lagrange-Newton constrained optimiser (for conical intersection searches only).
The trust radius approach (or line search) is controlled via the keyword
trustradius. Possible choices are:
- constant: Constant trust radius (equal to maxstep)
- energy: Trust radius based on the energy change
- gradient: Trust radius based on the projection of the gradient on
the current step. Can be used when no energy expression is available (e.g. NEB).
For optimisers requiring a Hessian, such as the Newton-Raphson or P-RFO algorithms,
the type of Hessian to be calculated is specified by the keyword
initial_hessian. Possible choices are:
- external: Calculate with the ChemShell routine $theory.hessian (default)
- onepoint: Build by one point finite difference of the gradient
- twopoint: Build by two point finite difference of the gradient
- diagonal: Build a diagonal Hessian by a single one point finite difference
- identity: Set the Hessian to be an identity matrix
In the case of initial_hessian=external, two point finite difference will be
used if an external Hessian is not available.
The Hessian will be updated depending on the
keyword update_method. Possible choices for update_method
are:
- bofill: Bofill update of the Hessian (default)
- powell: Powell update of the Hessian
- bfgs: BFGS update of the Hessian. (Note: this is a full BFGS Hessian update, not to be confused with the limited-memory version).
- none: No update, recalculate the Hessian in each step
2.4 Nudged elastic band options
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| neb |
keyword |
no |
no |
Specifies if and how the nudged elastic band method is to
be used. Can be no, free, frozen, or
perpendicular. |
| nimage |
integer |
no |
1 |
Specifies the number of images in a NEB
calculation. |
| neb_cart |
Boolean
|
no |
false |
Find the NEB starting path in the coordinate
system specified by coordinates, but switch to Cartesian coordinates for the
optimisation. |
| nebk |
real |
no |
0.01 |
Force constant for NEB calculations. |
| neb_climb_test |
real |
no |
3.0 |
Threshold for spawning the climbing image (as a
multiple of the gradient tolerance for convergence). |
| neb_freeze_test |
real |
no |
1.0 |
Threshold for freezing images during the optimisation (as a
multiple of the gradient tolerance for convergence). |
| weights |
Tcl List
|
no |
all 1 |
Weights specified as a Tcl list of real
numbers. One number for each atom.
The higher the weight for an atom, the more it contributes to the NEB path.
Atoms with weight=0 are excluded from the
transition mode. |
The keyword neb specifies that a nudged elastic band calculation
should be performed. The improved-tangent NEB algorithm with a climbing image
is implemented. Three versions are available:
- free: The endpoints of the NEB path are minimised
- frozen: The endpoints of the NEB path are frozen
- perpendicular: The endpoints of the NEB path minimised
perpendicular to the NEB path. Their distance to the nearest other point is
kept fix.
- neb= no no NEB is used.
The NEB path will be initiated as a linear transit between the geometries
specified by the keywords coords and coords2. The linear
transit will be calculated in the coordinate system specified by
coordinates. Sometimes it is preferable to initiate the path in
internal coordinates (in particular coordinates=tc) but to optimise
the path in Cartesian coordinates (more stable). In this case, specify
neb_cart=true.
The number of images is specified by nimage. The calculation will
start out without climbing image, thus with one image less than
nimage. Once the gradient perpendicular to the path is small enough (by default 3
times the general tolerance for gradient components), the climbing image will
be placed at the interpolated maximum of the path. From this point on, it will
be optimised with the rest of the path. Once the perpendicular force of an
image is smaller than the general tolerance for gradient components,
the respective image is frozen. This saves a significant number of energy
evaluations. The thresholds for
spawning the climbing image and freezing images can be set by neb_climb_test
and neb_freeze_test respectively. Setting them to 0.0 will switch off these
features, which may help if you experience convergence problems during the later
stage of the optimisation.
The use of the L-BFGS optimiser is recommended with NEB.
Additional output files may be written when using NEB. With
list_option=medium a file called nebinfo will be written after each
completed NEB step. It contains the path length to each image, the energy of
each image relative to the first image, and the work (gradient projected on the
path vector). The latter may be more relevant than the energy for huge
systems. Additionally a file nebpath.xyz is written. It contains the
present geometry of each image. ChemShell fragment files neb_*.c with the same
information are also written. With list_option=full additional files
neb_*.xyz are written containing the optimisation trajectory for each
image. These can be viewed e.g. with "vmd -m neb_*.xyz".
The NEB method may be run in parallel
using the task-farming framework.
2.5 Dimer method options
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| dimer |
Boolean
|
no |
false |
Specifies if the dimer method for TS search is to
be used. |
| dimer_interpolate |
Boolean
|
no |
true |
Specifies if the gradient in the dimer rotation
should be interpolated. |
| maxrot |
integer |
no |
10 |
Maximum number of dimer rotation steps before a
translation step. |
| tolrot |
real |
no |
5.0 |
Tolerance for dimer rotation (in degrees). |
| delta |
real |
no |
0.01 |
Dimer separation (in internal coordinates). |
| weights |
Tcl List
|
no |
all 1 |
Weights specified as a Tcl list of real
numbers. One number for each atom. The higher the weight for an atom,
the more it contributes to the
transition mode. Atoms with weight=0 are excluded from the
transition mode. |
The keyword dimer is used to start a transition state search using the dimer
method. Two images of the system (their distance is
specified by delta) are calculated. They are optimised along the
force in all directions perpendicular to the dimer axis, and against the force
along the dimer axis. Thus the system converges to a first order saddle point.
The translation of the dimer is optimised with the algorithm specified by
optimiser (L-BFGS is recommended). The rotation is optimised by a
conjugate gradient method.
After a rotation step, the gradient can be interpolated (default) or
recalculated (dimer_interpolate=false).
2.6 Conical intersection options
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| conint |
keyword |
no |
no |
Specifies if and how multi-state calculations are carried out.
Can be no, pf, gp, or
ln. |
| state_i |
integer |
no |
1 |
Choice of lower state for conical intersection optimisation. |
| state_j |
integer |
no |
2 |
Choice of upper state for conical intersection optimisation. |
| coupled_states |
Boolean
|
no |
yes |
Specify whether an interstate coupling gradient exists (if false, the coupling is set to zero). Only applicable to the gp and ln methods. |
| pf_c1 |
real |
no |
5.0 |
First weighting option for the penalty function term in the penalty
function conical intersection optimisation algorithm (in kcal/mol). |
| pf_c2 |
real |
no |
5.0 |
Second weighting option for the penalty function term in the penalty
function conical intersection optimisation algorithm (in kcal/mol). |
| gp_c3 |
real |
no |
1.0 |
Overall scaling of the gradient in the gradient projection
conical intersection optimisation algorithm. |
| gp_c4 |
real |
no |
0.9 |
Relative weighting of the two terms of the gradient in the
gradient projection conical intersection optimisation algorithm. |
| ln_t1 |
real |
no |
0.0001 |
Threshold for the Lagrange-Newton conical intersection
optimisation algorithm (in kcal/mol), below which orthogonalisation is switched on. |
| ln_t2 |
real |
no |
1.0 |
Threshold for the Lagrange-Newton conical intersection
optimisation algorithm (in kcal/mol), above which orthogonalisation is switched off. |
The keyword conint specifies that a conical intersection
optimisation should be carried out. At each cycle energies, gradients, and (if
applicable) interstate coupling gradients are calculated for two electronic
states. This information is used to search for a local minimum energy crossing
point between the states according to the chosen algorithm. The algorithms
available are:
- pf: Penalty function method
- gp: Gradient projection method
- ln: Lagrange-Newton method
- no: no multi-state calculation (default).
The states to be optimised are chosen using the options state_i and
state_j. Specific algorithm options can be set using pf_c1
and pf_c2 for the penalty function method, gp_c3 and
gp_c4 for the gradient projection method, and ln_t1 and
ln_t2 for the Lagrange-Newton method. The default values are those
recommended in the MNDO
implementation of these algorithms.
By default the gradient projection and Lagrange-Newton methods require the calling program to provide the interstate coupling gradient. However, if the interstate coupling gradient is zero by definition (for example, for states of different multiplicities), the algorithms can be used with the coupled_states option set to false, in which case only the two state gradients are required. The penalty function method never requires the interstate coupling gradient, but is usually less efficient than the other two methods.
Note that the pf and gp conical intersection optimisation
algorithms are independent of the choice of optimiser in principle
(in practice nr is recommended with bfgs updating).
The Lagrange-Newton method can only be used
with the Lagrange-Newton optimiser.
2.7 Population optimisation options
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| stochastic |
Boolean
|
no |
no |
Specifies if stochastic search is to be used. |
| genetic |
Boolean
|
no |
no |
Specifies if the genetic algorithm is to be used. |
| General options |
| po_pop_size |
integer |
no |
25 |
Working population size. |
| po_radius |
real |
no |
1.0 |
Maximum displacement when generating initial population. |
| po_tolerance_g |
real |
no |
0.001 |
Threshold for convergence of maximum component of gradient |
| po_maxcycle |
integer |
no |
10000 |
Maximum number of optimisation cycles (note maxcycle is ignored). |
| Stochastic search only |
| po_contraction |
real |
no |
0.9 |
Factor by which search radius is contracted at end of each cycle. |
| po_tolerance_r |
real |
no |
1.0e-8 |
Threshold for stopping optimisation based on search radius. |
| po_distribution |
keyword |
no |
force_bias |
Search strategy. Can be random, force_direction_bias or force_bias |
| po_scalefac |
real |
no |
10.0 |
Scaling factor for absolute gradient vector in force_bias strategy. |
| Genetic algorithm only |
| po_init_pop_size |
integer |
no |
2*po_pop_size |
Initial population size from which the lowest energy individuals are taken
to from the first working population. |
| po_reset |
integer |
no |
500 |
Number of cycles before resetting population. |
| po_mutation_rate |
real |
no |
0.15 |
Mutation rate (probability of displacement of a coordinate). |
| po_death_rate |
real |
no |
0.5 |
Death rate (probability of removing an individual). |
| po_nsave |
integer |
no |
10 |
Number of low-energy minima to store. |
Two population-based search algorithms are implemented in DL-FIND:
a genetic algorithm and stochastic search. Typically these are used to search
for global minima on the potential energy surface although the stochastic search
can also be used with a force bias to find local minima.
The genetic algorithm and stochastic search methods may be run in parallel
using the task-farming framework.
3. Microiterative optimisation
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| microiterative |
Boolean
|
no |
no |
Specifies if microiterative optimisation is to be used. |
| inner_atoms |
Tcl List
|
no |
none |
List of atoms in the inner region (which should contain all QM atoms). |
| inner_residues |
Tcl List
|
no |
none |
List of HDLC residues in the inner region (which should contain all QM atoms). Alternative to inner_atoms for HDLC optimisations.
|
| include_res |
Boolean
|
no |
no |
Specifies how to handle HDLC residues that cross the boundary between
inner and outer regions. If false, split any HDLC residues that cross the boundary into two.
If true, include the whole residue in the inner region. |
| maxmicrocycle |
integer |
no |
100 |
Maximum number of microiterative cycles
permitted before switching back to macroiterations. |
| micro_esp_fit |
Boolean
|
no |
no |
For microiterations,
approximate the QM region using charges fitted
to the electrostatic potential. qm_theory must be GAMESS-UK,
TURBOMOLE or MNDO. |
Microiterative optimisation methods improve the efficiency of QM/MM optimisation by
separating the active atoms into an inner region (which should contain the QM region)
and an outer environment. After each step taken in the inner region, the environment
is relaxed completely. The idea is to minimise expensive inner region (macroiterative)
evaluations at the cost of increasing the number of environment (microiterative) cycles.
Microiterative methods only save overall calculation time if QM region calculations
are not performed during the microiterations. If micro_esp_fit is set to true,
the electrostatic influence of the QM region will be approximated by fitting point charges at the
QM atom sites to an electrostatic potential generated by the QM code.
ESP fitting for microiterative optimisation is currently available in the
GAMESS-UK, TURBOMOLE and MNDO interfaces.
Microiterative optimisation has been implemented for minimisation with L-BFGS, transition
state optimisation with P-RFO and the dimer method, and reaction path optimisation with NEB.
In all cases the outer environment region is relaxed using L-BFGS. For the transition state
and reaction path methods, this is equivalent
to specifying spectator degrees of freedom (setting weights to zero) in a standard optimisation.
This is useful for eliminating complications that can be caused by irrelevant degrees of freedom.
For P-RFO this also means that the Hessian is only calculated over the inner degrees of
freedom, which can dramatically reduce the cost of the Hessian calculation.
4. Hessian calculations
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| thermal |
Boolean
|
no |
false |
Don't optimise. Calculate the Hessian and
thermal corrections to the enthalpy and entropy instead. |
| temperature |
real |
no |
300 |
Temperature (in Kelvin) at which thermal
coorections should be calculated. |
DL-FIND may also be used to calculate a finite-difference Hessian and
thermal corrections to the enthalpy and entropy. In this mode there is no optimisation stage.
If there are no frozen atoms, the rotational and translation modes are projected out
before determining the vibrational frequencies. If frozen atoms are found this projection is not
applicable but the softest modes can be selectively ignored in the
thermochemical analysis using the nzero option (default: 0).
Note that thermal calculations work in mass-weighted coordinates throughout. The
displacements used and resulting Hessian will therefore not agree exactly with
the output of a force module calculation
(even if the same masses and del value are specified), where the mass-weighted Hessian is
generated from an initial Cartesian Hessian.
The one-point or two-point finite-difference Hessian may be calculated in parallel
using the task-farming framework.
5. Rate Calculations
Reaction rates can be calculated in DL-FIND in two different ways: (1)
approximations which only use the energies and Hessians at a minimum
and a saddle point (transition structure) associated to it (i.e. rates
by harmonic transition state theory), and (2)
Instanton rates in which the most-likely tunnelling path is optimised.
| Argument |
Argument type |
Mandatory |
Default |
To specify |
| thermal |
Boolean
|
no |
false |
Don't optimise. Calculate the Hessian and
thermal corrections to the enthalpy and entropy instead. |
| rate |
Boolean
|
no |
false |
Don't optimise. Read Hessians of the
reactant state (RS) and the transition state (TS) and calculate
rates by different methods. No energy or gradient calculations are
performed. |
| qts |
Boolean
|
no |
false |
Search for an instanton path (a quantum transition state) |
| qtsrate |
Boolean
|
no |
false |
Calculate the Hessian of an instanton and the
instanton rate |
| tsplit |
Boolean
|
no |
false |
Calculate the tunnelling splitting. Only
applicable with qtsrate=true |
| inithessian |
integer |
no |
0 |
5: skip energy-and-gradient
calculations, read Hessian from file. 6: Read Hessian of individual
images from file |
| mass |
Tcl List
|
no |
masses of the most abundant isotope |
Atomic masses in atomic mass units
(m(C)=12). One entry per atom. The masses used are printed with list_option=debug |
| nzero |
integer |
no |
0 |
Number of modes assumed to have zero vibrational frequency |
5.1 Rates Calculated by Harmonic Transition
State Theory
The Hessians at both the reactant state (RS) minimum and the
transition state (TS) saddle point geometries have to be calculated
by setting thermal=true. This writes the files qts_reactant.txt and
qts_hessian_rs.txt in case of the reactant, and qts_ts.txt
and qts_hessian_ts.txt in case of the transition state. In case of
a TS, the crossover temperature Tc is calculated:
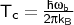
with
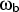 being the absolute value of the imaginary
frequency.
After the Hessians have been calculated, rates are calculated in an
independent run of dl-find by setting rate=true. The files qts_reactant.txt,
qts_ts.txt, and class.in have to be provided. The latter is an
input file of the following format:
being the absolute value of the imaginary
frequency.
After the Hessians have been calculated, rates are calculated in an
independent run of dl-find by setting rate=true. The files qts_reactant.txt,
qts_ts.txt, and class.in have to be provided. The latter is an
input file of the following format:
first line: ignored
second line: number of zero eigenvalues for the reactant and for the TS
(e.g. 6 6)
third line: starting temperature, end temperature, number of
temperature steps (e.g. 300. 150. 20}).
fourth line: T if bimolecular rates should be calculated.
The output (stdout or the file arrhenius) can directly
be used in an Arrhenius plot: the first column contains
1000/T in Kelvin, the next columns contain the
log10 of the rates in s−1
(cm3s−1 in case
of bimolecular rates) in the following
approximations:
- Classical rates
- Rates with quantised vibrations (which includes
the zero-point vibrational energy)
- Quantised vibrations plus tunnelling correction
via the simplified Wigner correction to second order:
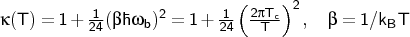
The rate with quantum vibrations is multiplied by the expression above.
- Exact analytical quantum rates for a
symmetric Eckart barrier fitted to the particular system (barrier
hight and
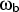 ). All degrees of freedom
perpendicular to the reaction coordinate are approximated as quantum
mechanical harmonic oscillators.
). All degrees of freedom
perpendicular to the reaction coordinate are approximated as quantum
mechanical harmonic oscillators.
- For temperatures above the crossover temperature Tc, the full
Wigner-corrected rates is also given:
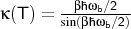
Another file called arrhenius_polywigner is written in
which the rate is calculated by simplified Wigner corrections to second (same
as above), fourth, sixth, and eighth order.
KIEs can be calculated directly by first running DL-FIND with
rate=true using the Hessians for the light
isotopologue. The file arrhenius of this run can be copied to
the file rate_H in the directory where the rate with heavier isotopes is to
be calculated. There, the same class.in as in the light case (at least the
same temperature parameters) should be used. The rates obtained with the
light nuclids are read and the KIE is directly calculated and written to a
file called kie.
5.2 Rates by Instanton Theory
Instanton theory is applicable for temperatures below Tc
for each system.
Optimisation of the first instanton starting from the
classical transition state structure (qts=true): The
file qts_hessian_ts.txt has to be renamed
to qts_hessian.txt. All geometrical data are read in
from qts_hessian.txt. However, coords
and coords2 still have to be provided (for historic
reasons, number of atoms, ...), but are ignored (as in all
instanton optimisations and rate calculations). A finite value of
distort specifies how far the images will be spread along the
unstable mode of the classical TS, see [1]. Newton–Raphson
optimisation (optimiser=NR) is recommended
[1, 2]. The number of images of the instanton path is
specified by nimage. Instanton search is activated by qts=true.
The NR optimiser was modified to avoid convergence to higher-order saddle
points [2]. This avoids the collapse of the instanton path to the
classical TS.
Instanton searches are performed in mass-weighted coordinates with masses
consistent with atomic units (electron mass, me). That is, the
mass of a hydrogen atom (1H) is 1837.15 me. This scales all
distances up by a factor of 42.695 (=(atomic mass
unit/me)1/2) compared to mass-scaled coordinates. Thus, the
tolerance criterion (tolerance) has to be smaller by the same
factor to achieve equivalent convergence. A tolerance of 10−7 (input as
1.E-7 in ChemShell) is usually sufficient, but convergence
even to a tolerance of 10−8 can often still be
achieved, which results in more reliable rates. Since NR converges quadratically, the more
stringent tolerance generally does not increase the number of steps
dramatically.
If NR (or P-RFO) is used, the updated Hessian will be used to
calculate a preliminary estimate of the rate (if
qts_reactant.txt is available). In that case,
qts_hessian_upd.txt will be written, which contains only
the updated Hessian. The file qts_coords.txt will be
written. It acts as input for subsequent recalculation of the
Hessian and a rate calculation.
Restarting instanton searches: Proper restart information (check files) is
not written for the time being. Using NR, a restart is possible, though, by
renaming qts_hessian_intermediate.txt (which is written after
each step) to qts_hessian.txt and starting the simulation
again. It will start from the Hessian and the geometry after the last full
set of energies has been obtained.
Instanton rate calculation (qtsrate=true): qts_coords.txt
from a previous instanton optimisation is read (coords and
coords2 are ignored). The temperature is also read from
qts_coords.txt. The rate calculation is selected by
qtsrate=true. Hessians at all images and the
rate are calculated as described in [2]. qts_hessian.txt is written, which acts as
input for subsequent instanton optimisations.
Restarting of rate calculations is also only possible by using the
Hessian information written for each image in
qts_hessian_imageX.txt. For these files to be read, set
inithessian=6.
Next instanton optimisation in sequential cooling: Starting from
qts_hessian.txt at a previous (in general higher) temperature,
another instanton is calculated. Distort should be zero, all other
parameters are the same as above. The number of images may be
increased. For optimal interpolation, the number of new images
Pn should be related to the number of old images Po
by Pn = k Po − k + 1
with k>1 being an integer. This ensures k−1 new images between each pair
of old images.
Instanton KIEs can be calculated by starting out from a Hessian
(qts_hessian.txt) for a different isotopologue and
changing the masses in the input. The Hessian will be re-weighted
accordingly. The instanton geometry has to be re-optimised. The file
qts_reactant.txt obtained with
changed masses can not be used. Instead, a file
qts_hessian_rs.txt can be provided. The Hessian of the
reactant obtained from that file will also be re-weighted.
In an approximation called fixed-path approximation (FPA) one can keep the instanton geometry fixed
and just change the masses [3]. This is done by calculating an instanton
rate with inithessian=5 (read the Hessian from file rather
than recalculating it) and changing the masses.
For lower temperature (compared to Tc) the number of
images necessary can be kept at bay by adapting the integration grid
to the potential energy along the instanton path [2]. This only
makes sense if the instanton path has reached the reactant
minimum. The adaptive grid
can be achieved by setting nebk=1 (This is not interpreted as
the NEB force constant, but as a parameter which can vary from zero to
one. One corresponds to a fully adaptive grid).
An instanton rate can be calculated from an existing Hessian (i.e. from the
file qts_hessian.txt) without any additional energy
calculations by setting inithessian=5.
Hessians of the individual images can be read in (all or just a part)
from files qts_hessian_imageX.txt) by setting inithessian=6.
5.3 Bimolecular Rates
Bimolecular rates are at the moment only implemented for one atom reacting
with a molecule. qts_reactant.txt refers to the reactant molecule. I.e. it
has 3 degrees of freedom less than the classical TS. qts_reactant.txt has to
be adapted manually: the energy of the incoming atom has to be added to the
third line (which contains the energy of the reactant molecule). Additionally,
the mass on the incoming atom (in atomic mass units) should be appended at the
third line (thus, two real values in the third line).
The relative partition function of the incoming atom will be calculated and
replaces the vibrational partition function for three degrees of freedom. The
rate is internally calculated in atomic units (as is the case for uni-molecular
reactions), but will be converted to molecules cm3 s−1 upon output.
5.4 Tunnelling Splittings
Tunnelling splittings of the vibrational ground state level can be
calculated by setting tsplit=true. Every time a rate is
calculated, the tunnelling splitting is calculated as well. Tunnelling
splittings only make sense for symmetric molecules and barriers.
5.5 References Covering the Implementation
of Tunnelling Rate Methods
The following references should be cited if the corresponding methods
are used:
- [1] Judith B. Rommel, T. P. M. Goumans, and Johannes
Kästner, J. Chem. Theory Comput., 2011, 7, 690. DOI: 10.1021/ct100658y
- [2] Judith B. Rommel, Johannes Kästner
J. Chem. Phys., 2011, 134, 184107. DOI: 10.1063/1.3587240
- [3] Jan Meisner, Judith B. Rommel and Johannes Kästner
J. Comput. Chem. 2011, 32, 3456. DOI: 10.1002/jcc.21930
6. Examples
- Minimisation in internal coordinates (DLC):
dl-find coords=c \
theory= mndo: $mndo_args \
coordinates=dlc \
result=minimum.c
- Transition-state search using the P-RFO algorithm (equivalient to "Baker"
in newopt):
dl-find coords=c \
theory= mndo: $mndo_args \
optimiser=prfo trustradius=const \
delta=0.01 update_method=bofill maxupdate=50 \
result=ts_prfo.c result2=tsmode_prfo.c tsrelative=true
- Minimisation with internal constraints. Note that internal constraints
(bonds, angles, ...) are only available in DLC and HDLC coordinates. Atoms can
be fixed (frozen) in all coordinate systems using the active_atoms or frozen options.
dl-find coords=c \
theory= mndo: $mndo_args \
coordinates=dlc \
constraints= { { bond 1 2 } { torsion 1 2 3 4 } }
- Nudged-elastic band:
It is recommended to use a larger tolerance in NEB calculations than in
normal TS search. The TS can subsequently be refined with the dimer method.
dl-find coords=rs.c coords2= { ts.c ps.c } \
theory= mndo: $mndo_args \
coordinates=cartesian \
optimiser=lbfgs trustradius=const \
neb=frozen nimage=10 nebk=0.01 \
tolerance=0.0045 \
maxcycle=400 maxene=3000 \
result=ts_neb.c restult2=tsmode_neb.c \
maxstep=0.9
- Dimer method for subsequent refinement of the NEB transition state:
dl-find coords=ts_neb.c coords2=tsmode_neb.c \
theory= mndo: $mndo_args \
coordinates=cartesian \
optimiser=lbfgs tolerance=0.00045 trustradius=const \
dimer=true delta=0.01 \
maxcycle=400 maxene=300 \
result=ts_dimer.c result2=tsmode_dimer.c \
maxstep=0.5
The transition mode can be visualised by writing a sequence in xyz format:
tsmode_xyz coords=ts_dimer.c coords2=tsmode_dimer.c \
n=20 delta=1. file=tsmode_dimer.xyz
- To minimise the system starting from a transition state, use the keyword
distort. Note that any coordinate system can be used
(e.g. coordinates=dlc) even though the transition mode has been
calculated in cartesians.
dl-find coords=ts_dimer.c coords2=tsmode_dimer.c distort=0.1 \
theory= mndo: $mndo_args \
coordinates=dlc \
optimiser=lbfgs trustradius=energy \
result=minimum.c
- Conical intersection optimisation using the Lagrange-Newton algorithm:
dl-find coords=c \
theory= mndo: $mndo_args \
coordinates=cartesian \
conint=ln state_i=1 state_j=2 \
optimiser=ln tolerance=0.00045 trustradius=const \
initial_hessian=diagonal update_method=bfgs maxupdate=1000 \
maxcycle=400 maxene=300 \
result=conint.c \
maxstep=0.1 minstep=0.0
Note that minstep should be set to zero as the Hessian must always be updated
to ensure that the Lagrange-Newton constraints are imposed. The ln optimiser must be
used with BFGS updates recommended.
- A potential-energy-surface scan is described in the tutorial.
|
![]()