STFC
MPI für Kohlenforschung

University College London

Programming Optimisation Schemes in Newopt

Introduction

The standard optimisation algorithms described above are written in terms of basic commands, which may be put to much more use in allowing the user to write his own Tcl script, which may contain things like if-statements and loops.

The most flexible way to use the package is thus to invoke the component commands directly from a Tcl script. To allow recursive or reentrant optimisation algorithms to be constructed, an object-oriented design has been adopted. An optimiser object is created using the optimiser command, the name of the object is then a valid Tcl command and methods are invoked by the syntax 

$opt <method>
Where opt is set to the name of the optimiser object and <method< is the name of the required method. The optimiser's internal data is stored in two types of data structure
  1. Control data is held in elements of the no_parm array.
  2. Numerical data is help in ChemShell Matrix objects.
Different instances of the optimiser are distinguished by using the optimiser name in both cases: The variables are referenced using names of the form no_parm($opt,<param_name>) and the matrix names are prefixed by the optimiser name.

Method Args Function
px   print current parameter position
sp   test point as suitable restart point-tester is the RMS of the gradient
ss   save the start structure (only for the zopt function, named zmatrix.start)
sr   save the best available structure (only for the zopt function, named zmatrix.best)
wr name write object to file, attaching label. Valid labels are start, best, vis
f   compute function value
g   compute gradient
fdg   compute gradient by finite-difference of energy
eg   compute gradient without frozen hessian eigenmode contributions
fg   compute function and gradient
gn   get current gradient norm (into parm(gnorm))
grms   get current gradient rms (into no_parm(grms))
tg   test quality of gradient
ug   transform gradient with hessian eigenvectors
h   compute analytic hessian (for gamess only)
fdh   generate hessian by finite differences of gradients with a one-point formula for all variables
fdh2   generate hessian by finite differences of gradients with a two-point formula for all variables
fd i generate hessian row and column for variable i by finite differences of gradients with a one-point formula
fd2 i generate hessian row and column for variable i by finite differences of gradients with a two-point formula
gh   generate diagonal guess-hessian from simple rules
efdh i j ... modify hessian by finite-differencing along i'th, j'th, k'th, etc. hessian eigenmodes and back-transform the hessian
efdh2 i j ... modify hessian by two-point finite-differencing along i'th, j'th, k'th, etc. hessian eigenmodes and back-transform the hessian
sh m set hessian matrix from matrix m
shv i a set diagonal hessian value for variable i to a
mh   condition hessian to have the correct inertia by massageing the eigenvalues
sih m set inverse hessian from matrix m
sh1   set hessian matrix to be the unit matrix
sih1   set inverse hessian to be the unit matrix
dh   diagonalise hessian
sm   set (first usage) or select (all subsequent usages) hessian eigenvector mode to be followed in TS search
sms   set (first usage) or map (all subsequent usages) hessian eigenvector modes unto starting modes
um   update hessian eigenvalue mode to be followed in TS search
hc   determine the hessian inertia ( i.e. the number of positive, negative, and zero eigenvalues)
ih   invert hessian
iih   invert the inverse hessian
dih   diagonalise inverse hessian
pu   Powell-update the hessian
bfu   BFGS-update the hessian
bfui   BFGS-update the inverse hessian using the GAMESS-UK code
u0   BFGS estimate and first update of the inverse hessian
u   BFGS-update the inverse hessian
msu   Murtagh-Sargent-update the hessian
msui   Murtagh-Sargent-update the inverse hessian
pmsu   Hybrid Powell/Murtagh-Sargent-update the hessian
s   take current step
ovls   calculate overlap between current and previous step
rx   reset the position vector to that of the previous step
sl s set step length to s
cl s calculate step length and set it to s if it exceeds s
clv s calculate search length and set it to s if it exceeds s
rs s restrict step, such that largest element equals s
tr   determine trust region by comparing actual and predicted energy changes
ee   estimate energy change from second-order model (valid hessian assumed)
gs   set step vector to steepest descent direction
es iv set step vector to inverse hessian eigenvector iv
evs iv set step vector to hessian eigenvector iv
pfm i project i'th hessian eigenvector (mode) out of the step-vector
gda   add current point to diis space
gdd i delete i'th (first point 0) point from diis space
gddg   delete point with highest gradient rms from diis space
gdp   print all current diis data points and gradients
gds   evaluate diis step
gdw   write diis space (points and gradients to files newopt.gdxr and newopt.gdgr, respectively
gdr m1 m2 read diis space from matrices m1 (points) and m2 (gradients)
cgr   calculate conjugate gradient restart step vector
cg   calculate conjugate gradient step vector (Shanno-Phua code)
cgs   calculate conjugate gradient step vector
n   set step vector by newton method
prfo   calculate (p)rfo step vector
ls   line search step
ls2   line search step with at least two trial points
lsf   line search step with function values only
lsg   line search step with function and gradient values
tc   check for convergence
d   diagnose the current point for sensibility
sym m symmetrize square matrix m
lv   list current variables and their gradients
pun name append the current structure to punch-file name for viewing
praxis   invoke PRAXIS optimizer
log   print optimisation log (steps, line searches, updates)
x   free memory

The above commands operate on a group of Matrix data structures, listed in the following table. In many cases it is not necessary to access the data explicitly--since an entire optimisation can be performed in terms of the operations given above. However, a series of Tcl commands are available if one wants to operate on the Matrix data structures directly.

Tag Dimensions Title
$opt.f 1 x 1 f (function value)
$opt.pf 1 x 1 pf (previous function value)
$opt.x n x 1 x (position vector)
$opt.px n x 1 px (previous position vector)
$opt.rx n x 1 rx (best restart position vector)
$opt.g n x 1 g (gradient vector)
$opt.pg n x 1 pg (previous gradient vector)
$opt.gd n x 1 gd (gradient difference [g - pg])
$opt.eg n x 1 eg (gradient vector for convergence test)
$opt.v n x 1 v (current search dir)
$opt.s n x 1 s (step vector)
$opt.ps n x 1 ps (previous step)
$opt.h n x n h (hessian matrix)
$opt.ph n x n ph (previous hessian matrix)
$opt.ih n x n ih (inverse hessian matrix)
$opt.evalh n x 1 evalh (eigenvalues of hessian matrix)
$opt.evech n x n evech (eigenvectors of hessian matrix)
$opt.ug n x 1 ug (transformed gradient vector)
$opt.m n x 1 m (mode-following vector)
$opt.mode n x 1 mode (mode vector)
$opt.modes n x n modes (modes (original hessian eigenvectors))
$opt.st n x 1 st (step vector from CG restart iter)
$opt.yt n x 1 yt (g(i) - g(i-1) from CG restart iter)
$opt.yi n x 1 yi (current g(i)-g(i-1))

NOTE: $opt.st, $opt.yt, and $opt.yi are defined only in a conjugate-gradient optimisation.

The following table describes the elements of the Tcl array no_parm that are used to control the operation of the primitive commands. The first series of elements may be set during the optimisation; the second series are generated by the various commands and may be accessed to control the optimisation. The default values, where given, are those applied in the control scripts, (as invoked by the newopt and hessian commands. When writing custom optimisation algorithms many will need to be set explicitly.

Element Usage Default
function function to be invoked  
args Tcl list of arguments to be passed to the function  
method type of calculation finite_difference ( hessian); bfgs ( newopt)
threshold threshold-value for recalculation of hessian for selected degrees of freedom  
status Tcl return value 0
verbose output flag 0
del displacement in finite-difference formulae 0.001
maxstep maximum number of steps in search 200
conv_maxgrad maximum gradient convergence criterion 0.001
conv_rmsgrad RMS gradient convergence criterion 0.0002
conv_maxstep maximum parameter step convergence criterion 0.001
conv_rmsstep RMS parameter step convergence criterion 0.0002
toler_energy energy forced-convergence criterion 1.0e-10
list_variables full listing of variables after each step yes
step maximum step-length 0.3
lsopt type of line-search algorithm ls
ls_eps1 line-search convergence parameter 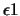$\epsilon1$ 0.9
ls_eps2 line-search convergence parameter 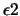$\epsilon2$ 0.001
trust_region vary maximum step length according to predictive power of the second-order model inactive
stepmin minimum step length with trust-region method 0.01
stepmax maximum step length with trust-region method 0.5
follow_mode hessian eigenvalue mode to be followed in TS search (use normal counting) 0 ( i.e. minimisation)
update_mode redefine mode to be followed to be the step taken off (keep starting mode)
hessian_update define update method of the hessian powell
fin_diff_eigenmodes recalculate part of the hessian by finite-differencing selected eigenmodes if inertia deteriorates no
keep_correct_hessian disregard update if hessian inertia deteriorates no
recompute_hessian number of steps after which hessian is to be recomputed maxstep+1 ( i.e. no recalculation of the hessian)
recompute_method method by which to compute the hessian finite_difference
condition_hessian hessian conditioning off
run_diagnostics check sensibility of the current point off
old_energy energy of previous point  
new_energy energy of current point  
best_step index of step with lowest RMS gradient  
trust_steps number of steps taken without RMS gradient getting smaller 10
set_restart flag to write best restart structure after each step yes
thresh_prfo threshold for contribution of hessian eigenmodes to prfo step 1.e-4
conv_prfo convergence criterion for prfo shift parameter 1.e-4
contribute_prfo cutoff on hessian eigenvalue for contributing modes to prfo bracketing scheme 1.e-4
freeze_soft_modes flag for freezing near-zero eigenvalue hessian modes in Baker algorithm 0
soft_mode criterion on eigenvalue for considering a hessian eigenmode soft 1.e-3
freeze_modes flag for freezing selected hessian modes in Baker algorithm 0
mode_list Tcl list of indices of modes to freeze " "
min_diis_dimension minimum size of GDIIS space  
max_diis_dimension maximum size of GDIIS space nvar/2
read_diis_space flag for reading in GDIIS matrices 0
diis_positions name of matrix with GDIIS positions " "
diis_gradients name of matrix with GDIIS gradients " "
maxlength maximum allowed step length 0.3
nvar number of degrees of freedom in the optimisation problem  
hessian_ok indicator of correct hessian inertia no
best_hessian number of incorrect hessian eigenvalues  
pos number of positive hessian eigenvalues nvar
gnorm gradient norm  
grms gradient rms  
map_modes Tcl list of map of current hessian eigenmodes on starting modes  


Using The method=custom option

When a custom optimisation method is required, it can be passed in the form of Tcl list to the newopt procedure, as shown below. Note that the commands execute in a context in which the variable opt is set to the name of the optimiser object. 
newopt function=$func method=custom \
	commands = { $opt fg; $opt gs; $opt ls; $opt u0; $opt n;
           while { [ $opt tc ] != 1 } { $opt ls; $opt u; $opt n; } 
        }

Constructing New optimisation procedures

It is sensible to use the optimisation algorithms within ChemShell for guidance, e.g. see chemsh/src/newopt/newopt_bfgs.tcl.

This manual was generated using htp, an HTML pre-processor Powered by htp